Numerický model požární zkoušky v peci
Článek popisuje virtuální pec pro zkoušení požární odolnosti konstrukcí. Jedná se o numerický model stropní pece vytvořený v programu FDS (Fire Dynamics Simulator), který je založen na metodě CFD (Computational Fluid Dynamics). Přesnost numerického modelu je validována pomocí několika požárních zkoušek provedených ve vodorovné peci v požární laboratoři PAVUS, a.s. Výsledky v podobě teploty plynu uvnitř pece vykazují dobrou shodu s experimenty, a to i v případě přítomnosti hořlavého zkušebního vzorku. Využití numerického modelování na základě analýzy dynamiky plynů se proto ukázalo jako vhodná metoda pro modelování zkoušek požární odolnosti.
1. Úvod
Pasivní požární ochrana staveb je tvořena stavebními konstrukcemi a jejich schopností odolávat účinkům požáru (požární odolnost konstrukcí). Požární odolnost konstrukcí se může stanovit podle tabulek, výpočtem nebo zkouškou v akreditované zkušebně. Požární odolnost je dána mezními stavy a klasifikační dobou, po kterou je stavební konstrukce schopna odolávat účinkům požáru.
Stanovení požární odolnosti konstrukcí pomocí zkoušky bývá finančně velmi nákladné. Nicméně se tímto způsobem může zjistit požární odolnost konstrukcí, které mohou obsahovat nové materiály nebo mají atypické tvary a není tak možné je zařadit podle tabulek nebo stanovit jejich požární odolnost výpočtem.
Požární zkoušky se provádí v akreditovaných evropských zkušebnách. V České republice je takto akreditována zkušebna PAVUS, a.s. ve Veselí nad Lužnicí. Zkoušky požární odolnosti se provádí na horizontálních a vertikálních neboli stropních a stěnových pecích. Vytvořením numerického modelu pece vhodnými softwary je možné dosáhnout snížení počtu požárních zkoušek a redukovat tak jejich vysoké finanční náklady.
2. Zahraniční práce
První aplikaci metody CFD při modelování pece pro zkoušku požární odolnosti konstrukcí lze nalézt již v roce 1997 ve Velké Británii. Pomocí softwaru SOFIE (Simulation of Fires in Enclousures) byl odborníky na univerzitě vytvořen model stěnové pece. Pec byla zahřívána podle normové teplotní křivky (ISO 834). Zkoušeným vzorkem byla ocelová deska, která byla vložena doprostřed zkušební pece. Teplota plynu byla měřena pomocí osmnácti termočlánků. Výsledky ukázaly vyšší teploty v numerickém modelu oproti křivce ISO 834. Tato studie ukázala velký potenciál ve využití metody CFD pro modelování zkoušek požární odolnosti konstrukcí [1].
Později byl numerický model pece vytvořen v Portugalsku v roce 2009. Cílem této práce bylo zjistit rozložení teplot uvnitř pece o vnitřním objemu 1 m3 za pomocí šestnácti deskových snímačů teploty (dále jen DST). Na této malé peci byl proveden experiment s termočlánky. Plyn byl ohříván podle křivky ISO 834. Numerický model vytvořený v programu ANSYS Fluent odhalil lokální účinky hořáků na rozložení teploty v peci, ale celkové výsledky byly srovnatelné s provedeným experimentem [2].
Další z modelů pece pochází z roku 2011 z Francie. Použitým softwarem byl FDS5. Teplota a tlak v modelované peci byly řízeny podle normových požadavků EN 1363-1 na zkoušení požární odolnost. Následně byl model pece v FDS propojen se softwarem CAST3M. Toto propojení softwarů bylo použito pro návrh požární odolnosti sendvičových fasádních panelů [3].
Ve studii z Turecka z roku 2016 je popsán numerický model pece o vnitřním objemu 1 m3. Za pomocí programu ANSYS Fluent byly zkoumány účinky větracího otvoru v peci na vliv teploty. Výsledná teplota byla porovnána s křivkou ISO 834. Z výsledků studie bylo zřejmé, že v počátcích simulace byl odtah plynů nedostatečný a v peci byly vyšší teploty oproti křivce ISO 834 [4].
3. Experimentální studie
3.1. Popis pece
Obr. 1 Stropní pec v požární zkušebně PAVUS, a.s.
V rámci grantu č. 16-18448S proběhlo několik experimentálních zkoušek pro validaci numerického modelu. Experimenty se prováděly v požární zkušebně PAVUS, a.s. ve Veselí nad Lužnicí. Zkoušky byly realizovány v horizontální peci (obr. 1). Pec má vnitřní rozměry 3,0 m × 4,0 m v půdorysu a 2,16 m na výšku. Stropní pec je ohřívána osmi plynovými hořáky, vždy čtyřmi na obou delších stranách. Palivem pro ohřev pece je směs zemního plynu a vzduchu.
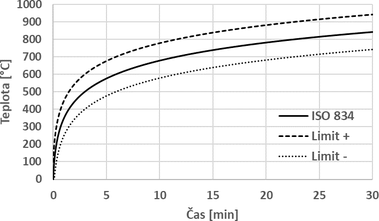
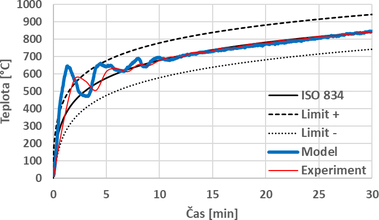
Nejčastěji se pec ohřívá podle nominálních teplotních křivek. Řízení teploty probíhá pomocí DST umístěných 0,1 m pod stropem. Tyto DST řídí na základě zjištěných teplot výkony hořáků. Výkony hořáků je možné regulovat podle průměrné teploty z řídících DST nebo jednotlivě přiřadit hořák ke konkrétním DST. Tento způsob je velmi efektivní a ve stropní peci se dosahuje velmi přesných teplot podle nominálních křivek. Při zkoušení požární odolnosti podle nominální normové teplotní křivky jsou podle normy ČSN EN 1363-1 v prvních 30 minutách dány limity ±100 °C oproti ISO 834 [5]. Na obr. 2 je zobrazena normová teplotní křivka s povolenými limity. Rovnice normové teplotní křivky je:
kde hodnota t je doba v minutách od začátku požární zkoušky.
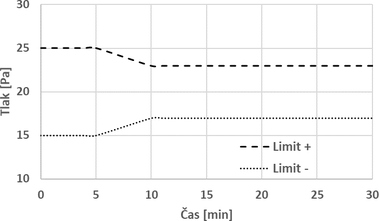
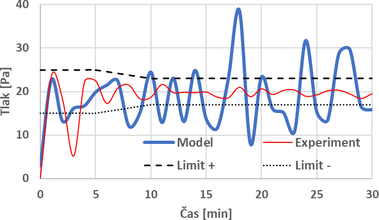
Neméně důležitým parametrem je měření přetlaku v peci oproti okolnímu tlaku vzduchu. Samotné měření se provádí snímačem na zadní straně pece ve výšce 1,38 m nad podlahou. Rozdíl hodnoty tlaků uvnitř a vně pece je dán normou ČSN EN 1363-1. Tato hodnota rozdílu přetlaků je 20 Pa. Norma dovoluje limity přetlaku ± 5 Pa do 5. minuty a ± 3 Pa od 10. minuty zkoušky (obr. 3) [5]. Regulování tlaku pece probíhá přes obdélníkový otvor v podlaze a následným nuceným odtahem přes ventilátor potrubím vně pece. Odvodem pomocí tohoto otvoru se reguluje přetlak v peci, aby tak odpovídal normovým požadavkům.
Obr. 2 Normová teplotní křivka s limity
Obr. 3 Limity přetlaku
Obr. 4 Deskový snímač teploty a plášťový termočlánek 100 mm pod stropem
3.2. Měření teploty v peci
V průběhu všech provedených experimentálních zkoušek byly měřeny teploty 16 DST a 25 plášťovými termočlánky typu K. Během všech experimentů byly DST i plášťové termočlánky vždy na stejné pozici tak, aby bylo možné ověřit vliv zkušebních vzorků na průběh teploty. Termočlánky byly umístěny v několika výškových a řezových rovinách. Na obr. 4 je zobrazeno měřící místo nacházející se 0,1 m pod stropem. V tomto místě je vidět dvojice obou typů termočlánků – plášťového termočlánku i DST.
4. Validační zkoušky
K ověření přesnosti modelu byla provedena série tří experimentů. Prvním experimentem byla zkouška v prázdné peci. Zkouška byla provedena ve 2 variantách. Při první variantě byl plyn v peci zahříván podle normové teplotní křivky. V druhé variantě byla pec ohřívána pomocí nástavného konstantního výkonu hořáků. Tento experiment sloužil pro získání a následné nastavení hodnot výkonů hořáků pro numerický model. Dále bylo při zkoušce zjištěno rozložení teplot v peci bez vlivu zkoušeného prvku.
Druhým experimentem byla zkouška s ocelovým nosníkem IPE 400 (obr. 5). Nosník byl zavěšen na čtyřech závitových tyčích podélně pod stropem pece tak, aby mezi ním a stropem pece nevznikala vzduchová mezera. Naměřené průběhy teplot zahrnovaly vliv zkušebního vzorku.
Třetím experimentem byla zkouška s třemi lepenými dřevěnými nosníky průřezu 100 mm × 240 mm (obr. 6). Tyto nosníky byly uloženy v příčném směru, tedy kolmo na delší strany pece. Nosníky byly zavěšeny pod strop pece tak, aby mezi stropem a jejich vrchním povrchem nevznikala vzduchová mezera. V rámci experimentu proběhlo několik dalších měření a pozorování. První nosník byl opatřen na spodních rozích čtyřmi ocelovými „L“ úhelníky. Druhý nosník byl opatřen čtyřmi obdélníkovými plechy kotvenými svorníky vždy po dvou na svislých stranách nosníku a třetí byl ponechán bez úpravy.
Obr. 5 Zkouška s ocelovým nosníkem
Obr. 6 Zkouška s dřevěnými nosníky
5. Numerický model
Numerický model je vytvořen pro stropní pec pro zkoušku požární odolnosti stavebních konstrukcí v PAVUS, a.s. ve Veselí nad Lužnicí. Jedná se o pec, na které byly provedeny výše zmíněné experimenty. Pro vytvoření numerického modelu byl zvolen program FDS 6.5.4. Jedná se o program, který je založen na matematické metodě modelování CFD. Software FDS je mimo jiné schopen simulovat tyto fyzikální jevy: dynamiku plynů při hoření zahrnující přestup tepla prouděním a sáláním, pyrolýzu pevných částic nebo hoření plynných produktů a mnoho dalších [6]. Program FDS je proto vhodný pro vytvoření numerického modelu pece pro zkoušku požární odolnosti konstrukcí. Jako vizualizační program je použit Smokeview 6.4.2 [7].
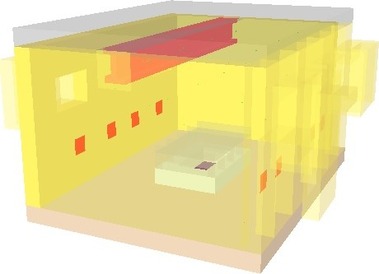
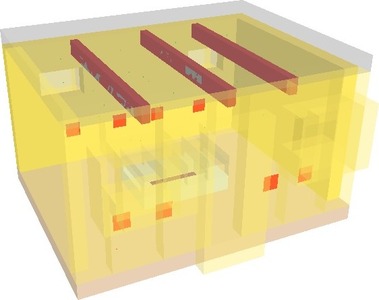
Modelování ve vybraném softwaru umožňuje vytvořit konkrétní případ simulace zkoušky v peci. Z tohoto důvodu je vytvořen zdrojový kód pro každý experiment. V zásadě se jednotlivé modely od sebe neliší, jsou pouze přidány nebo odebrány zkušební vzorky a jejich měřící zařízení. Na obr. 7 a 8 jsou vizualizace dvou virtuálních zkoušek. Jednotlivé konstrukce použité v modelu pece jsou vytvořeny z materiálů, které odpovídají skutečné peci. Důležitým nastavením numerického modelu pece je nastavení tepelně technických vlastností materiálů v závislosti na teplotě.
Obr. 7 Model s ocelovým nosníkem
Obr. 8 Model s dřevěnými nosníky
5.1. Palivo a výkon hořáků
Ve virtuální peci je nastaveno stejné palivo jako je tomu ve skutečné peci – směs zemního plynu a vzduchu. V programu FDS je možné definovat hořlavou plynnou látku příkazem „REAC“, která vstupuje do reakce hoření [8]. Palivo pro reakci hoření v FDS je zvolen metan CH4, který je hlavní složkou zemního plynu. Do reakce hoření vstupuje vzduch definovaný procentuálním obsahem kyslíku O2, dusíku N2, vlhkosti H2O a oxidu uhličitého CO2. Aby chemická rovnice byla úplná, jsou definovány produkty hoření s jejich procentuálním zastoupením [6]. Numerický model obsahuje následnou chemickou reakci hoření [6]:
Hodnota výkonu hořáků ve virtuální peci je určena podle dat získaných během experimentálních zkoušek. V reálné peci je výkon hořáků řízen podle teploty naměřené DST100 mm pod stropem, tak aby teplota odpovídala normové teplotní křivce. Z experimentální studie bylo zjištěno, že maximální výkon jednoho hořáku je 4256 kW/m2. U numerických modelů je stanovena maximální hodnota výkonu hořáků z průměru všech osmi hořáku.
Obr. 9 Tepelný výkon hořáku v modelu
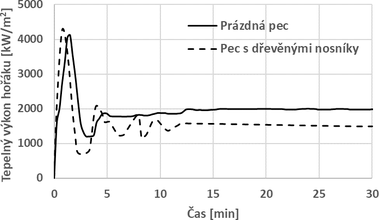
V případě modelu s dřevěnými nosníky, kdy dochází k hoření zkušebních vzorků, je výkon hořáků nižší. K celkovému přírůstku teploty uvnitř pece přispívá energie z hoření těchto nosníků. V modelu bylo proto nutné nastavit odhořívání dřevěných nosníků. Na obr. 9 je porovnání výkonu jednoho hořáku modelu bez zkoušeného vzorku a modelu s dřevěnými nosníky. Na tomto grafu je vidět, že křivka výkonu u modelu s dřevěnými nosníky je nižší. Rozdíl mezi těmito průběhy je v pokročilé fázi simulace necelých 500 kW/m2. Tento rozdíl ve výkonu je dán příspěvkem hořením dřevěných nosníků. Hořáky proto nemusí mít nastavený tak vysoký výkon jako je tomu v případě pece bez vzorku.
5.2. Ventilace
Velmi důležitou částí numerického modelu je nastavení ventilace pro udržení rozdílu přetlaku 20 Pa hořících plynů v peci oproti okolnímu tlaku vzduchu. Pro sledování hodnoty přetlaku ve virtuální peci je v modelu přítomen snímač ve výšce 1,4 m nad podlahou a 0,1 m od zadní stěny. Virtuální pec má rovněž otvor v podlaze pro odvod plynů o velikosti 0,6 m × 0,8 m odpovídající velikosti výpočetní sítě v simulaci.
V případě otevřeného otvoru v podlaze po celou dobu simulace dochází k samovolnému úniku přetlaku z pece ven. Toto řešení se však po prozkoumání vypočtených hodnot přetlaku ukázalo jako nedostatečné. Numerický model byl následně doplněn o prvek simulující odtahový ventilátor, který má za úkol přebytečný přetlak odebrat. Princip ventilátoru ve virtuální peci odpovídá principu ventilátoru ve skutečné peci. Ventilátor je aktivován a deaktivován automaticky v závislosti na zadaných limitních hodnotách přetlaku uvnitř pece. Pro model virtuální pece se jako efektivní hodnoty spodního a horního limitu ukázaly hodnoty 18 Pa a 20 Pa. Vlivem setrvačnosti účinnosti zařízení ve virtuální peci jsou limity v modelu jiné než normové hodnoty. Nicméně díky těmto mezním hodnotám dojde k nejefektivnější regulaci přetlaku mezi limitními hodnotami danými normou. Druhou důležitou hodnotou, která se ukázala jako vhodná, je nastavení množství odváděného plynu vně pece. Tato hodnota je dána množstvím odváděného vzduchu za jednotku času a je stanovena na 4,0 m3/s po celou dobu trvání simulace experimentů.
Shodně jako ve skutečné peci i v modelu je přidána ocelová konstrukce nad ventilačním otvorem (obr. 10 a 11). Tato konstrukce v reálné peci chrání ventilační otvor před padajícími částmi zkušebních vzorků, zároveň také ovlivňuje směr proudění odtahovaného plynu. Díky této ocelové konstrukci je odtahovaný plyn odebírán z boku ochranné konstrukce, a ne přímo z místa nad otvorem, tedy prostředku pece. Přítomnost tohoto prvku ve virtuální peci je proto velmi důležitá.
Obr. 10 Ventilační otvor s ochrannou konstrukcí ve skutečné peci
Obr. 11 Ventilační otvor ve virtuální peci
6. Validace modelu
6.1. Model bez zkušebního vzorku
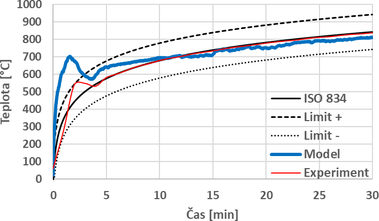
Model požární zkoušky bez zkušebního vzorku slouží k ověření správnosti nastavení výkonu hořáků ve virtuální peci a nastavení řízení přetlaku a jeho regulování pomocí ventilátoru v otvoru podlahy. Funkčnost modelu je validována pomocí výsledků experimentů provedených ve zkušebně PAVUS, a.s. ve Veselí nad Lužnicí. Sledovaným parametrem je teplota plynu v peci. Průběh této veličiny musí stejně jako u reálných zkoušek odpovídat podmínkám daných normou ČSN EN 1363-1. Na obr. 12 a 13 jsou uvedeny grafy porovnání teploty plynu z modelu a experimentu. Obr. 12 rovněž znázorňuje ISO křivku a limity dané normou ČSN EN 1363-1.
Obr. 12 Teplota plynu – zkouška podle ISO 834
Obr. 13 Teplota plynu – zkouška s konstantním výkonem hořáků
Z obou grafů je patrné, že teploty v numerickém modelu jsou v počáteční fázi vyšší, než je tomu při experimentech. U modelu s ohřevem podle normové teplotní křivky je teplota v prvních dvou minutách vyšší o téměř 150 °C oproti experimentu. Tento jev může být mimo jiné způsoben netěsností skutečné pece (stropní panely a jejich spoje), kde může určité množství tepla uniknout z pece ven. Modelovaná pec má zcela těsnou stropní konstrukci a nedochází zde k žádnému úniku tepla. Nicméně po čase 5 minut simulace se teploty blíží k hodnotám z experimentu a rozdíly jsou maximálně 30 °C.
V případě zkoušky s konstantním výkonem hořáků nejsou rozdíly naměřených hodnot tak vysoké. Maximální rozdíl teplot v pokročilejší době simulace je cca 20 °C. V počáteční fázi ale stále dochází k rychlejšímu ohřevu u numerického modelu. Úpravou křivky výkonu hořáků v počáteční fázi ohřevu by mohlo dojít k přiblížení se k naměřeným teplotám z experimentu. Na základě porovnání teplot plynu je patrné, že nastavení hořáků podle maximálního výkonu je správný krok z hlediska celkového průběhu simulace.
6.2. Model pece s ocelovým nosníkem
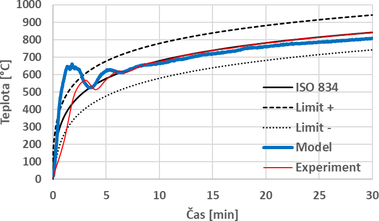
Validace modelu je shodně jako v předchozím případě provedena pomocí průměrné teploty z podstropních DST. Obr. 14 zobrazuje průběh teplot z numerického modelu a z experimentu. Graf je opět doplněn o normovou teplotní křivku a limity povolené normou ČSN EN 1363-1. Je patrné, že i v tomto případě je v počáteční fázi simulace teplota výrazně vyšší než během experimentu. Po uplynutí 5 minut dochází ke srovnání obou křivek a model má stejný průběh teploty jako při experimentu. Od 8. minuty simulace dochází k nepatrnému odchýlení sledované křivky. V čase 30 minut je teplota plynu o cca 30 °C nižší. Na obr. 15 jsou zobrazeny průběhy přetlaku v peci naměřené během experimentu a vypočítané v modelu. Z grafu je patrné, že ve virtuální peci dochází k lokálním výkyvům přetlaku uvnitř pece.
Obr. 14 Průměrná teplota plynu 0,1 m pod stropem
Obr. 15 Průběh přetlaku během zkoušky
6.3. Model pece s dřevěnými nosníky
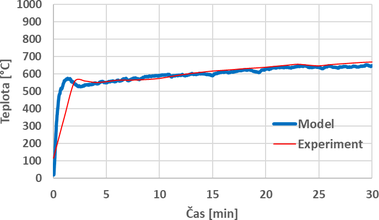
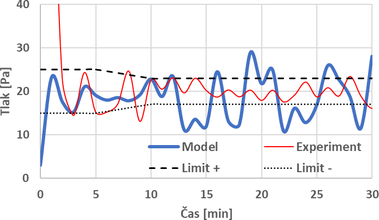
Třetím validovaným modelem je virtuální pec s třemi dřevěnými nosníky. U tohoto modelu je měřena teplota plynu na stejných pozicích, jako tomu je u předchozích modelů. Validace je opět provedena pomocí průměrné teploty z DST umístěných pod stropem. Jejich porovnání je na obr. 16. Z grafu je vidět, že v případě tohoto modelu nedochází k tak výraznému nárůstu teploty v počáteční fázi, jako tomu bylo u předchozích modelů. Opět se ukazuje, že nastavení hořáků podle průměrných hodnot z experimentů je správný krok a je možné si jej na tomto porovnání ověřit. Porovnání průběhů tlaku ve virtuální peci a experimentu je na obr. 17. V počáteční době simulace je přetlak v modelu mezi normovými limity. Po uplynutí 12 minut dochází k opětovnému překračování limitů, jako tomu bylo u předchozích modelů.
Obr. 16 Průměrná teplota plynu 0,1 m pod stropem
Obr. 17 Průběh přetlaku během zkoušky
7. Závěr
Z uvedených výsledků je patrné, že virtuální pec prokazuje dobré výsledky především v pokročilé době simulace, kde se teploty plynu téměř shodují s experimenty. Virtuální pec vykazuje dobrou shodu i v modelu s dřevěnými nosníky. V tomto případě je však nutné zadat vhodnou reakci hoření dřeva a funkci uvolňování tepla z hořlavého materiálu.
Zvolená metoda CFD a program FDS se ukázaly jako vhodné prostředky pro předpověď teplot v peci pro zkoušení požární odolnosti konstrukcí, mimo jiné i s hořlavými zkušebními vzorky. Pomocí pokročilého sdruženého modelu, který je založen na propojení dynamické analýzy plynů (CFD modelu) s metodou konečných prvků (MKP), tak lze virtuální pec využít k ověření požární odolnosti konstrukcí. Sdružený model může vést ke snížení financí zejména u opakujících se zkoušek požární odolnosti. Nicméně k širšímu využití např. požárními zkušebnami je potřeba model dále zdokonalovat. Další výzkum je proto zaměřen na nastavení a efektivní řízení ventilace tak, aby nedocházelo v modelu k překračování limitních hodnot stanovených normou. Dále na automatické řízení hořáku podle měřených teplot z deskových snímačů teploty, tak jak je tomu v případě reálné zkoušky a na studii citlivosti sítě, která hraje důležitou roli zejména v případě přítomnosti hořlavých zkušebních vzorků v peci.
Poděkování
Výzkum uvedený v tomto článku byl podpořen projektem 16-18448S Sdružený model požární zkoušky v peci (GAČR). Autoři by rovněž rádi poděkovali pracovníků požární zkušebny PAVUS, a.s.
Literatura
- WELCH, S. a RUBINI, P. A. Three-dimensional Simulation of Fire-Resistance Furnace. Melbourne, Australia: Proceedings of 5th International Symposium on Fire Science, 1997.
- PILOTO, P. A. G., MESQUITA, L. M. R. a PEREIRA, A. A. Thermal analysis in fire-resistance furnace. Santander, Spain: Proceedings of the International Workshop on Fire Protection and Life Safety in Buildings and Transportation Systems, 2009.
- CAYLA, F., LEBORGNE, H. a JOYEUX, D. Application of a virtual resistance furnace: fire resistance test simulation of a plasterboard membrane. Prague: ASFE Conference, 2011.
- KARABAŞ, O., a et al. Numerical Investigation of Temperature Distribution in a Fire Resistance Test Furnace. Alanya/Antalya: 4th International Symposium on Innovative Technologies in Engineering and Science, 2016.
- ČSN EN 1363-1. Zkoušení požární odolnosti – Část 1: Základní požadavky. Praha: ÚNMZ, 2013.
- McGRATTAN, K. et al. Fire Dynamics Simulator (Version 6), User's Guide. Maryland, USA: National Institute for Standards and Technology, 2014.
- FORNEY, G. P. Smokeview, A Tool for Visualizing Fire Dynamics Simulation Data (Version 6), User's Guide. Maryland (USA): National Institute for Standards and Technology, 2014.
- WALD, F., a další. Modelování dynamiky požáru v budovách. Praha: České vysoké učení technické v Praze, 2017. ISBN 978-80-01-05633-2.
The article describes a virtual furnace for fire resistance test of structures. The virtual furnace is a numerical model of a ceiling furnace created in FDS (Fire Dynamics Simulator) program, which is based on the Computational Fluid Dynamics (CFD) method. The numerical model is validated by the aid of several fire tests carried out in a horizontal furnace at the fire laboratory PAVUS, a.s. Results of the gas temperature within the furnace show good agreement with the experiments, even in the case of presence of a flammable test specimen. The use of numerical modeling based on fluid dynamics analysis has been therefore proven to be a suitable method for modeling fire resistance tests.
