Nejnavštěvovanější odborný web
pro stavebnictví a technická zařízení budov
estav.tvnový videoportál

TZB-info / Bezpečnost budov / Požární bezpečnost staveb / Empirické modely charakteristik nebezpečí výbuchů a požárů, odhad charakteristik a kategorizace staveb

Empirické modely charakteristik nebezpečí výbuchů a požárů, odhad charakteristik a kategorizace staveb

Ing. Otto Dvořák, Ph.D., VŠB TUO FBI Ostrava, externí školitel
Recenzovaný

Článek uvádí možnosti výpočetních odhadů vybraných charakteristik požárů havarijně uniklých plynů a kapalin, konkrétně tryskových požárů, mžikových požárů (vzplanutí), požárů kaluží a ohňových koulí. Člení modely požárů a výbuchů na empirické, fenomenologické a CFD s příklady konkrétních typů dostupných modelů a kategorizace pozemních staveb podle normových tříd následků. V závěru je zdůrazněn význam těchto výpočtů pro kvantitativní hodnocení rizik výbuchů a následných požárů. Článek navazuje na předchozí text s názvem Empirické modely charakteristik výbuchů a požárů a jejich scénáře, který shrnuje scénáře havarijních úniků plynů a kapalin.

1.Výpočty účinků požárů havarijně uniklých plynů/par/prachů

Havarijně uniklé hořlavé plyny po určitém rozptýlení ve vzduchu mohou generovat požár jako vzplanutí (tzv. Flash fire), tryskový požár (jet fire), uniklé kapaliny nebo zkapalněné hořlavé plyny mohou generovat požár louže (pool fire) či ohňovou kouli (Fireball) [3], [4], [18].

1.1 Tryskové požáry

Tyto požáry vznikají hořením havarijně unikajících plynů z tlakového zařízení. Hlavní jejich nebezpečí spočívá v sálání tepla od plamenů v místech jejich působení. Výpočetně se odhadují jejich [3]:

a) výška, L podle rovnice (15)

L / dt = 5,3 / CT . vzorec 15 (15)
 

kde je

L
délka viditelného turbulentního plamene od bodu úniku (m),
dt
průměr trysky (m),
CT
molový zlomek koncentrace hořlavých látky (HL) ve stechiometrické směsi se vzduchem (bezr.),
Tap, Thl
adiabatická teplota plamene a teplota proudu hořlavé látky (K),
αT
moly reaktantu vztažené na moly zplodin pro stechiometrickou směs hořlavá látka – vzduch,
Mv
molární hmotnost (kg/kmol),
Mhl
molární hmotnost hořlavé látky (kg/kmol),
 

b) intenzita toku tepla sáláním, Es podle rovnice (16)

Es = βa . Qs . Fz = βa . η . ṁ . ∆H0 . Fz (16)
 

kde je

Es
intenzita toku tepla sáláním v bodu terče (J/(m2.s)),
βa
propustnost vzduchu (bezrozm.),
Qs
celkový tepelný výkon zdroje sáláním (J/s),
Fz
faktor zorného pole bodového zdroje = 1/4πx2 (m−2), kde x je vzdálenost (m), od bodového zdroje k terči, viz obr. 4,
η
podíl celkové energie převedené na sálání (bezrozm.),
ṁ
hmotnostní průtok hořlavé látky (HL), (kg/s), viz např. [15],
∆H0
spalné teplo HL (kJ/kg).
 

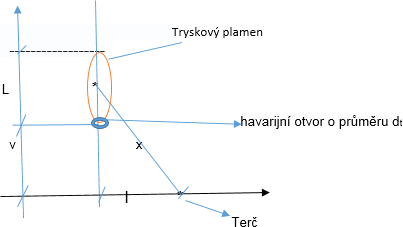
Obr. 4 Schéma tryskového plamene působícího na terč (např. osobu)
Obr. 4 Schéma tryskového plamene působícího na terč (např. osobu)
 

Tryskový plamen má ústí o průměru dt ve výšce v (m) nad zemí. Dosáhl podle rovnice (15) výšky L (m). Vzdálenost x (m) od bodového zdroje plamene (v ½ jeho výšky) k pozici působení na terč je rovna x = [(L / 2 + v)2 + l2 ]1/2

1.2 Požáry jako vzplanutí

Podle NFPA 2112 [14] jde o typ krátce trvajícího požáru, který vzniká při havarijním úniku paliva (plynu, prachu nebo par hořlavé kapaliny) rozptylujícího se ve vzduchu bez generování škodlivého přetlaku po zapálení, protože se plameny šíří vzniklým oblakem podzvukovou rychlostí a nedochází k výbuchu. Je charakterizován vysokou teplotou s krátkým trváním. Vdechnutí horkého vzduchu může vážně poškodit plíce s potenciálem možného udušení. Požár je velmi nebezpečný v uzavřených prostorách, neboť i když je relativně malý, může kontakt s plameny způsobit popáleniny a protože hoření spotřebuje přítomný kyslík s tvorbou kouře, může generovat udušení přítomných osob. Tento typ požáru ve formě krátkodobého vzplanutí může nastat i na operačních sálech v prostředí s hořlavými parami desinfekčních prostředků, obohaceného kyslíkem a za přítomnosti zápalných zdrojů (lasery, elektrická zařízení).

1.3 Požáry kaluží

Havarijní úniky kapalin s teplotami pod jejich normálními body varů často končí jako kaluže (ohraničených vodorovných hladin na povrchu). Pokud je unikající kapalina pod tlakem, který převyšuje její normální bod varu, tak část se bude mžikově vypařovat na páry a zbývající část kapaliny bude tvořit kaluž. Takto vytvořené kaluže vytvářejí rostoucí oblak par kapalin se vzduchem, což platí i pro kapaliny, které byly v zařízení pod tlakem jejich normálního bodu varu. Oblak je s velkou pravděpodobností zapálen iniciátorem v sousedství. Vzniklý požár kaluže je nebezpečný pro osoby a objekty v sousedství sáláním tepla plamenů a generováním oblaků kouře s nebezpečnými zplodinami hoření a sazemi. Tyto ničivé účinky jsou funkcí druhu hořlavé kapaliny, geometrie kaluže, doby trvání požáru a vzdálenosti terčů ohrožení.

Přímo nad okraji kaluže je jasně hořící, nesazující zóna s místy kde jsou nejvyšší intenzity sálání povrchu plamenů. Nasáváním vzduchu se tvoří víry, pulzace plamenů v radiálním i axiálním směru s tvorbou sazí. Pulzující část/zóna plamenů je propojena se svou bází, ale teploty plamenů na čele se mění. Častým předmětem výpočetních odhadů nebezpečí požárů kaluží jsou mimo jiné hmotnostní rychlost hoření (mh), maximální průměr kaluže (Dmax), výška plamene (H), geometrický faktor zorného pole bodového zdroje (Fz), průměrná hustota toku tepla sáláním (Epr), terčem obdržená hustota toku tepla sáláním (Eo), viz např. [15]. Pro výpočetní odhad těchto veličin lze aplikovat např. následující rovnice:

mh = 1.10−3 . ΔHv / ΔH (17)
 

kde je

mh
hmotnostní rychlost hoření (kg/m2.s),
ΔHv
výhřevnost (kJ/kg),
ΔH
výparné teplo kapaliny při bodu varu (kJ/kg),
 

Dmax = 2 . vzorec 18 (18)
 

kde je

Dmax
maximální průměr kaluže (m),
V̇L
objemový průtok unikající kapaliny (m3/s),
ẏ
rychlost odhořívání kapaliny (m/s),
 

H / D = 42 . vzorec 19 (19)
 

kde je

H
viditelná výška plamene (m),
D
ekvivalentní průměr kaluže (m),
mh
hmotnostní rychlost hoření (kg/m2.s),
ρv
hustota vzduchu (1,2 kg/m3 při 20 °C a 1 atm),
g
tíhové zrychlení (9,81 m/s2),
 

Fz = 1/4πx2 (20)
 

kde je

Fz
geometrický faktor zorného pole bodového zdroje (m−2)
x
vzdálenost (m) od bodového zdroje v plameni k terči působení,
 

Epr = Em . e−SD + Ek . (1 − e−SD) (21)
 

kde je

Epr
průměrná hustota toku tepla sáláním (kW/m2),
Em
max. hustota toku tepla sáláním svítících bodů (asi 140 kW/m2),
Ek
hustota toku tepla sáláním kouře (asi 20 kW/m2)
S
experimentální parametr (0,12 m−1),
D
průměr kaluže (m),
 

Eo = Ƭa . Qr . Fz = Ƭa . η . mh . ∆Hs . A . Fz (22)
 

kde je

Eo
terčem obdržená hustota toku tepla sáláním (kW/m2),
Qr
celkový vývin tepla hořením (kJ/s),
Fz
geometrický faktor zorného pole bodového zdroje (bezrozm.),
Ƭa
atmosférická propustnost (m−2),
η
podíl energie hoření uvolněná sáláním (obvykle 0,15 až 0,35),
mh
hmotnostní rychlost hoření (kg/m2.s),
∆Hs
spalné teplo hořlavé kapaliny (kJ/kg)
A
celková plocha kaluže (m2).
 

Autor ověřil výpočet podle uvedených rovnic (16)–(19) pomocí excelovské tabulky se vstupními daty a výsledky výpočtů uvedených v příloze 2. Aplikace je jednoduchá a po dosazení vstupních dat a vzorců je výsledek výpočtu okamžitý.

1.4 Ohňová koule BLEVE

Fyzikální výbuch BLEVE provází s velkou pravděpodobností zapálení hořlavého oblaku a vznik ohňové koule (OK), u které jsou výpočetně odhadovány maximální průměr (Dmax), doba trvání (tk), výška středu ohňové koule (H) a počáteční průměr polokoule na úrovni povrchu (Dpoč), např. podle následujících rovnic [3], [4]:

Dmax = 5,8.m1/3 (23)
 

tk = 0,45 . m1/3 pro m < 30 000 kg (24)
 

tk = 2,6 . m1/6 pro m > 30 000 kg (25)
 

Dpoč = 1,3 . Dmax (26)
 

kde je

Dmax
maximální průměr ohňové koule (m),
m
počáteční hmotnost hořlavé kapaliny (kg),
tk
doba trvání (s),
Dpoč
počáteční průměr polokoule na úrovni povrchu (m).
m
počáteční hmotnost hořlavé kapaliny (kg).
 

Kromě nebezpečí vzniklé tlakové vlny, viz uvedené rovnice, je ohňová koule nebezpečná sáláním tepla do okolí.

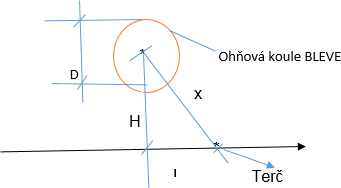
Obr. 5 Pozice ohňové koule (OK) pro výpočet Et (např. na osobu)
Obr. 5 Pozice ohňové koule (OK) pro výpočet Et (např. na osobu)
 

Nejčastěji je odhadována intenzita sálání tepla z povrchu OK podle rovnice (27) a intenzita sálání tepla na terč podle rovnice (28):

Ep = r . m . ΔHv / (π . D2max . tok) (27)
 

kde je

Ep
intenzita sálání z povrchu OK (W/m2)
r
podíl sálání tepla z tepla hoření (bezr.),
m
počáteční hmotnost hořlavé látky v OK (kg),
∆Hv
výhřevnost hořl. látky (J/kg),
Dmax
maximální průměr OK (m),
tok
doba trvání OK (s),
 

Et = 2,2 . Ƭvzd . r . ΔHv . m2/3 / (4πx2) (28)
 

kde je

Et
intenzita sálání tepla na terč (W/m2)
Ƭvzd
transmitance vzduchu (bezr.),
∆Hv
výhřevnost HL (J/kg),
r
podíl sálavého tepla z tepla hoření (bezr.),
m
počáteční hmotnost hořlavé látky v OK (kg),
x
vzdálenost ze středu OK do terče (m).
 

1.5 Shrnutí dostupných technik modelování požárů a výbuchů

Pro hodnocení rizik požárů a výbuchů je v současné době publikována řada modelů, viz např. [3], [4], [19], [23]. Liší se rozsahem aplikací, přesností, cenou a náročností (CFD) a rozsahem vstupních parametrů. Počítačové modely CFD navazují na výpočetně jednodušší výpočty empirické, viz rovnice uvedené pro výpočty základních parametrů výbuchů a na ně navazujících požárů. Lze je obecně členit na modely:

  • Empirické: jsou založeny na analýze experimentálních dat. V uživatelské praxi jsou hojně využívány:
    • TNT model ekvivalence,
    • Baker–Strehlowa metoda,
    • Metoda více energetického přístupu,
    • Metoda odhadu (podle Sedwick Energy Ltd).
  • Fenomenologické: jde o zjednodušené fyzikální modely výbuchu pod označením např.:
    • SCOPE (Shell Code for Over-pressure Prediction in gas explosion), verze 2 a 3,
    • CLICHE (Confined Linked Chamber Explosion).
  • CFD (Computational Fluid Dynamics) modely: jsou numerickým řešením diferenciálních rovnic, kterými jsou popsány dotčené procesy požáru nebo výbuchu: dynamika proudění tekutin a toku tepla a kouře na zvolené počítačové síti. Lze uvést např.:

Na rozdíl od empirických modelů CFD modely vyžadují nákup SW, absolvování školení práce se SW za úhradu a v neposlední řadě pokud možno inženýrskou znalost mechaniky proudění tekutin a řešené problematiky.

2. Nebezpečí výbuchu pro stavby a osoby

Pokud jsou hořlavé kapaliny nebo zkapalněné hořlavé plyny pod tlakem v nádobě, nádrži, lahvích, nastane jejich havarijní únik do přilehlé atmosféry např. z důvodu koroze pláště nádoby, výrobní závady, vnitřního neregulovaného přehřátí, vnějšího nárazu nebo působením vnějšího požáru s mžikovým vypařováním unikající vroucí kapaliny. Vzniklé páry/plyny zvyšují původní objem kapalin asi 200×, což generuje tlakovou vlnu a vystřelení úlomků/fragmentů nádoby.

Když tlaková/rázová vlna dopadne na povrch objektu, který není vodorovný ve směru jejího šíření, tak se odrazí, zesiluje a vytváří odražený tlak. Ten se mění s úhlem dopadu, a když je kolmý, tak je tlak odražené vlny maximální. Velikost tohoto maxima je funkcí též velikosti dopadajícího pmax , doby od výbuchu (ms), hmotnosti a druhu havarijně uniklé hořlavé látky a vzdálenosti od místa výbuchu. Nárazový přetlakový impulz ip (MPa.ms) je míra energie výbuchu působící na plochu nárazu. Výbušné tlaky významně klesají se vzdáleností od epicentra výbuchu. Poškození budovy bývá proto výrazně větší na přilehlé straně než na straně odvrácené. Již malé přetlaky však mohou způsobit velké škody, neboť přetlak např. 0,1 bar odpovídá síle 1 t/m2. Rozlišuje se výbuch probíhající v uzavřeném prostoru a otevřeném prostoru. Škody způsobené přetlakem výbuchu na běžných stavbách přibližuje tabulka v příloze č. 3 [3]. S ohledem na možné ničivé účinky výbuchu musí být navrhovány pozemní stavby tak, aby se celá stavba ani její podstatná část nezřítila, tj. aby měla dostatečnou robustnost. Norma ČSN EN 1991-1-7 [20] za tímto účelem kategorizuje pozemní stavby podle následků poruch konstrukcí nebo jejich částí do tříd 1, 2a, 2b a 3, viz tab. 2.

Tab. 2 Kategorizace pozemních staveb podle tříd následků [20]
Třída následkůPříklady kategorizace podle typů pozemních staveb a jejich používání
1
malá		Samostatné obytné domy do 4 NP. Zemědělské stavby. Stavby s občasným výskytem osob za předpokladu, že každá část takové stavby je vzdálena od další obytné budovy nebo oblasti navštěvované lidmi alespoň 1,5násobek výšky stavby.
2a
střední skupina
menšího rizika		Samostatné pěti podlažní obytné domy. Hotely do 4 NP. Budovy s byty, apartmány a další rezidentní budovy do 4 NP. Administrativní budovy do 4 NP. Průmyslové stavby do 3 NP. Obchodní plochy do 3 NP a s plochou každého podlaží maximálně 1 000 m2. Školní zařízení o 1 NP. Veškeré budovy nepřesahující 2 NP, kde je povolen vstup veřejnosti a plocha jednotlivých podlaží je nejvýše 2 000 m2.
2b
střední skupina
většího rizika		Hotely, budovy s byty, apartmány a další obytné budovy vyšší než 4 NP, avšak nejvýše 15 NP. Školská zařízení vyšší než 1 NP, avšak nanejvýš 15 NP. Obchodní plochy vyšší než 3 NP, ale nejvýše o 15 NP. Nemocnice do 3 NP. Administrativní budovy vyšší než 4 NP, avšak nejvýše 15 NP. Všechny budovy s přístupem veřejnosti a s plochou vyšší než 2 000 m2, avšak na každém podlaží maximálně 5 000 m2. Parkoviště nanejvýše o 6 NP.
3
velká		Všechny stavby, které přesahují omezení jednotlivých podlaží a jejich počtu ve třídách následků 2a a 2b. Všechny stavby, kde se shromažďuje značný počet osob. Stadiony s více než 5 000 diváky. Stavby s nebezpečnými látkami nebo technologickými procesy.

Norma upřesňuje mimo jiné, že konstrukce: třídy 1 se posuzovat nemusí, třídy 2 a 3 se musí posoudit ekvivalentním statickým výpočtem, třídy 3 musí být navíc posouzeny dynamickým výpočtem. Zatížení zásobníků a nádrží specifikuje norma ČSN EN 1991-1-4 [21]. Pro výpočetní odhady přetlaku na čele vzdušné tlakové vlny na základě odhadu redukované vzdálenosti a dále doby trvání průběhu kladné periody přetlaku lze aplikovat mimo jiné rovnice (6)–(8). Problematiku protivýbuchové ochrany staveb přehledným způsobem vysvětluje příručka M. Černína [22].

Ohroženi výbuchem jsou i osoby buď přímo úderem tlakové vlny nebo nepřímo úlomky/fragmenty. Nárazy přetlakové vlny o velikosti asi 103,4 kPa jsou smrtelné a při přetlaku 21 kPa se uvádí úmrtnost 50 % v důsledku krvácení v plících. Zranění letícími fragmenty je funkcí jejich hmotnosti a rychlosti při nárazu. Předpokládá se usmrcení fragmenty o kinetické energii 100 J.

3. Závěr

Cílem tohoto a předchozího článku „Empirické modely charakteristik výbuchů a požárů a jejich scénáře“ bylo uvést empirické rovnice, které lze v praxi snadno realizovat s dostupnými vstupními daty pro výpočetní odhady základních charakteristik výbuchů a následných požárů po havarijním úniku plynů, prachů a kapalin pro potřebu kvantitativních analýz jejich rizik. Vypočtené hodnoty jsou zatíženy nejistotami v závislosti na nejistotě vstupních dat a zjednodušení výpočtů např. předpokladem ideálního chování plynů a par. Konkrétní hodnoty výsledků empirických rovnic lze porovnat pro vybrané scénáře s výsledky výpočtů podle pokročilých, současně platných verzí CFD modelů, a s výsledky experimentů ve zmenšeném měřítku. Rozdíly v nejistotách těchto výsledků jsou publikovány v rozsahu (15–30) %. Výbuchy musí být zvažovány při navrhování všech částí pozemních a inženýrských staveb, kde se používají/budou používat, skladovat či přepravovat hořlavé plyny/kapaliny/prachy. Chyby lidského činitele při projektování, realizaci stavby a provozování objektů je nutno minimalizovat zvyšováním odbornosti pracovníků, jejich znalostmi kvalitativních a kvantitativních rizik a v neposlední řadě důslednými preventivními kontrolami.

Literatura

  1. NEDĚLNÍKOVÁ, H.: Požáry od výbuchů s únikem NCHL v ČR (výtah ze statistiky požárů). Praha: MV – GŘ HZS ČR, 2019.
  2. Statistická ročenka 2019 – Česká republika. Praha: MV – GŘ HZS ČR, 2020.
  3. Guidelines for Chemical Process Quantitative Risk Analysis. N. York, USA CPS – American Institute of Chemical Engineering, 2000.
  4. SFPE Handbook of Fire Protection Engineering.
  5. ČSN ISO 8421-1: 1996. Požární ochrana – Slovník – Část 1: Obecné termíny a jevy požáru.
  6. ČSN EN 1127-1 ED2: 2012. Výbušná prostředí – Zamezení a ochrana proti výbuchu – Část 1: Základní pojmy a metodologie.
  7. ČSN EN 15967: 2012. Stanovení maximálního výbuchového tlaku a maximální rychlosti výbuchového tlaku plynů a par.
  8. ČSN EN 60019-20-1:2010. Výbušné atmosféry - Část 20-1: Materiálové vlastnosti pro klasifikaci plynů a par – Zkušební metody a data.
  9. ČSN EN 14034-1 + A1:2011. Stanovení výbuchových charakteristik rozvířeného prachu – Část 1: Stanovení maximálního výbuchového tlaku pmax rozvířeného prachu.
  10. ČSN EN 14034-2 + A1:2011. Stanovení výbuchových charakteristik rozvířeného prachu – Část 2: Stanovení maximální rychlosti nárůstu výbuchového tlaku (dp/dt)max rozvířeného prachu.
  11. ČSN EN 14034-3 + A1:2011. Stanovení výbuchových charakteristik rozvířeného prachu – Část 3: Stanovení dolní meze výbušnosti rozvířeného prachu.
  12. ČSN EN 14034-4 + A1:2011. Stanovení výbuchových charakteristik rozvířeného prachu – Část 4: Stanovení mezní koncentrace kyslíku LOC rozvířeného prachu.
  13. ČSN EN 1839, ed. 2: 2017. Stanovení mezí výbušnosti a mezní koncentrace kyslíku pro hořlavé plyny a páry.
  14. NFPA 2112: 2018. Standard on Flame Resistant Clothing for Protection of Industrial Personnel Against Short-Duration Thermal Exposure from Fire.
  15. DVOŘÁK, O.: Výpočetní odhady havarijních úniků plynů a kapalin. Praha: TZB-info, 9. 3. 2020.
  16. DVOŘÁK, O.: Trojúhelníkové výbuchové diagramy hořlavých látek a jejich praktická využitelnost. Praha: časopis 112, ročník XVII, č. 3, 2018.
  17. DVOŘÁK, O.: Požární charakteristiky pro pokročilé modelování požárů. Praha: TZB-info, 9. 3. 2020.
  18. AICHE/CCPS: 1994. Guidelines for Evaluation of the Characteristics of Vapour Cloud Explosions, Flash Fire and BLEVES.
  19. A Guidance Manual for Modelling Hypothetical Accidental Release to the Atmosphere. American Petroleum Institute, Washington, 1996.
  20. ČSN EN 1991-1-7:2007. Euro kód 1: Zatížení konstrukcí – Část 1-7: Obecná zatížení – Mimořádná zatížení. ČNI.
  21. ČSN EN 1991-1-4:2007. Euro kód 1: Zatížení konstrukcí – Část 1-4: Zatížení zásobníků a nádrží. ČNI.
  22. ČERNÍN, M. a kol.: Příručka proti výbuchové ochrany staveb. Nakladatelství ČVUT v Praze, 2008.
  23. DVOŘÁK, O. a kol.: Vývoj a validace požárních modelů pro stanovení vývinu a šíření tepla, kouře, toxických plynů a tlakových vln pro simulace a interpretace scénářů požárů/výbuchů a jejich ničivých účinků. DVZ výzkumného projektu č. VD20062010A07. Praha: MV-GŘ HZS ČR-TÚPO, 2009.

Příloha 2

Příklad aplikace rovnic (16)–(19) s výpočtem hustoty toku tepla sáláním z hořící kaluže hořlavé kapaliny se vstupními daty v tabulce
Vstupní data
objemový průtok unikající kapaliny0,1m3/s
spalné teplo kapaliny43700kJ/kg
výparné teplo kapaliny300kJ/kg
bod varu kapaliny363K
teplota okolí298K
hustota kapaliny730kg/m3
tepelná kapacita kapaliny (konst.)2,5kJ/kg.K
průměr kaluže25m
vzdálenost terče od kaluže50m
relativní vlhkost50%
účinnost sálání pro model bodového zdroje0,35
Výsledky výpočtů
modifikované výparné teplo462,5kJ/kg
svislá rychlost hoření1,20E−04m/s
hmotnostní rychlost hoření0,087598kg/m2.s
maximální průměr kaluže32,57m
průměr pro výpočet25m
plocha kaluže490,87m2
poměr H/D plamene1,59
výška plamene39,72m
parciální tlak vodních par1579,95Pa
model bodového zdroje
výška bodového zdroje19,86m
vzdálenost k terči působení77,58m
geometrický faktor zorného pole1,32E−05m−2
propustnost0,70
intenzita toku tepla sáláním na terč6,12kW/m2

Příloha 3

Tlak (kPa)Odhad škod tlakovou vlnou na objektu
0,21občasné rozbití velkých skleněných oken
0,69–1,03rozbití malých oken
2,07určité poškození stropů domů
2,76drobné stavební destrukce
3,4–6,9okna jsou vždy zničená, poškození rámů oken a menší poškození konstrukcí domů
6,9částečná demolice domů, která je činí neobyvatelnými
6,9–13,8odpad dřevěných a vlnitých kovových panelů
9,0slabě deformované ocelové nosné konstrukce budovy
13,8částečné zborcení stěn a střech domů
13,8–20,7zničení betonových nebo škvárobetonových panelů
15,8dolní mez vážného poškození stavebních konstrukcí
17,2destrukce cihelného zdiva budov z 50 %
20,7těžké stroje v průmyslové budově jsou poškozeny, ocelový rám budovy je deformován a stržen ze svých základů
20,7–27,6celoocelové samonosné panely budovy jsou zbourány, prasknutí stěn skladovacích nádrží
27,6prasknutí obvodových plášťů průmyslových budov
34,5prasknutí dřevěných víceúčelových sloupů
34,5–48,2téměř komplexní destrukce budov
48,2převržení naložených vlakových vagonů
68,9pravděpodobně úplná destrukce budov, těžkých strojů
English Synopsis
Empirical models of explosion and fire risk characteristics, estimation of characteristics and categorization of buildings

The article presents the possibilities of computational estimates of selected characteristics of fires of accidentally escaping gases and liquids, namely jet fires, instant fires (flashes), pool fires and fireballs. It divides fire and explosion models into empirical, phenomenological and CFD with examples of specific types of available models and categorization of buildings according to standard classes of consequences. Finally, the importance of these calculations for the quantitative assessment of the risks of explosions and subsequent fires is emphasized.

 
 
Reklama