Aplikace pro výpočet rozložení teploty v betonové desce vystavené požáru
Algoritmus programu TeDisOn pro řešení problému vedení tepla v betonové desce vystavené požáru je založen na metodě konečných diferencí a je implementován v programovacím jazyku JavaScript. Grafické uživatelské rozhraní pro zadávání uživatelem definovaných parametrů a pro interpretaci výsledků je vytvořeno pomocí jazyka HTML. Článek dále stručně představuje algoritmus použitý ve vytvořené aplikaci a prezentuje použití webové aplikace na třech různých příkladech. Z prezentovaných výsledků je zřejmé, že nově vyvinutá webová aplikace je uživatelsky přívětivá, lehce dostupná a velmi rychlá.
1. Úvod
Rozložení teploty v betonové desce vystavené požáru lze získat vyřešením problému vedení tepla. Problém vedení tepla v betonových konstrukcích vystavených požáru lze popsat standardním modelem neustáleného vedení tepla, viz např. (Štefan 2015) a tam uvedené reference. Tento model je silně nelineární (vlivem okrajových podmínek a materiálových vlastností) a obecně jej nelze analyticky vyřešit. Různí autoři pro řešení problému navrhli a použili různé numerické přístupy, viz např. (Štefan 2015) a tam uvedené reference. Největší výhodou těchto přístupů je, že řešení lze získat relativně snadno.
Nejčastěji používané numerické přístupy jsou založeny na metodě konečných prvků nebo metodě konečných rozdílů. Metoda konečných prvků je podrobně popsána a použita pro řešení problému transportu tepla v práci (Štefan 2015). Tato metoda je poměrně složitá a výpočetně náročná; je však velmi vhodná pro problémy se složitou geometrií a okrajovými podmínkami. Metodu konečných rozdílů lze sice snadněji implementovat a je mnohem rychlejší; je však vhodná pouze pro problémy s jednoduchou geometrií. Podrobný popis metody konečných rozdílů lze nalézt například v publikaci (Bažant & Jirásek 2018). Použití metody konečných rozdílů pro řešení problému vedení tepla v betonových konstrukčních prvcích vystavených požáru lze nalézt např. v (Hertz 2012).
V dnešní době je patrná snaha vytvářet inženýrské výpočetní programy jako webové (internetové) aplikace, viz např. (Civil Calculation 2020), (EurocodeApplied.com 2020), (using Eurocodes 2020). Výhodou webových aplikací je to, že je lze spustit na téměř jakémkoliv zařízení (např. stolní počítač, notebook, mobilní telefon atd.) a v jakémkoliv operačním systému (např. Windows, Linux, MAC, Android atd.) bez nutnosti instalace. Webové aplikace jsou tedy snadno použitelné a uživatelsky přívětivé.
1.1 Motivace
Přestože numerické přístupy k řešení transportu tepla v betonových konstrukcích vystavených požáru již byly vytvořeny a implementovány jinými autory, autor této práce nenalezl žádnou vhodnou webovou aplikaci pro řešení tohoto problému. Hlavním cílem této práce je vytvoření snadno dostupné a intuitivně využitelné webové aplikace pro řešení tohoto problému, tj. stanovení rozložení teploty v betonové desce vystavené požáru. Dalším cílem je představení vytvořené aplikace na konkrétních příkladech. Tento článek navazuje na výsledky prezentované v (Holan & Štefan 2019).
2. Metody
Pro řešení problému transportu tepla v betonové desce vystavené požáru je použit standardní model neustáleného vedení tepla
kde ρc(θ) [kg/m3] je objemová hmotnost betonu, cp,c(θ) [Jkg/K] tepelná kapacita betonu, θ [K] je teplota a λc(θ) [Wm/K] je tepelná vodivost betonu. Měrná tepelná kapacita, tepelná vodivost a objemová hmotnost betonu za vysokých teplot jsou uvažovány dle (ČSN EN 1992-1-2 2006). Okrajové podmínky jsou uvažovány jako smíšené, tzn. že tepelný tok se uvažuje od přestupu a od radiace dle (ČSN EN 1991-1-2 2004)
kde q [W/m2] je tepelný tok, αc [W/m2K] je součinitel přestupu tepla prouděním, T [K] je teplota povrchu, T∞ [K] je teplota okolního prostředí, ε [−] je emisivita povrchu a σSB [W/m2K] je Stefan-Boltzmannova konstanta. V rovnici popisující okrajové podmínky je uvažována hodnota emisivity betonu dle (ČSN EN 1992-1-2 2006). Teplota okolního prostředí a součinitel přestupu tepla během požáru jsou uvažovány dle normové teplotní křivky (ISO-834) popsané v (ČSN EN 1991-1-2 2004). Problém rozložení teploty v betonové desce vystavené požáru lze zařadit do kategorie numericky jednodušších problémů s jednoduchou geometrií. Z tohoto důvodu byla pro řešení problému použita metoda konečných rozdílů, viz (Bažant & Jirásek 2018), (Hertz 2012). Pomocí této metody byl vytvořen výpočetní algoritmus.
3. Webová aplikace
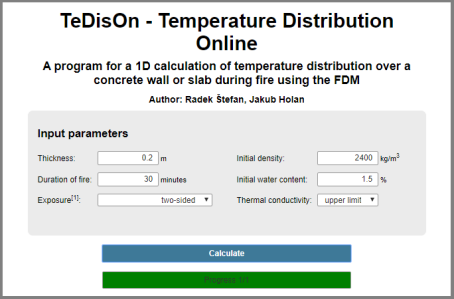
Obr. 1: Grafické uživatelské rozhraní pro zadání vstupních hodnot (Štefan & Holan 2020)
Pro dosažení snadné dostupnosti a využitelnosti výpočetního algoritmu byla vytvořena webová aplikace (Štefan & Holan 2020) implementací výpočetního kódu pomocí programovacího jazyka JavaScript. Grafické uživatelské rozhraní je vytvořeno pomocí jazyka HTML, viz Obr. 1. Pomocí tohoto rozhraní lze nastavit vstupní hodnoty pro výpočet. Do programu lze zadat tloušťku konstrukce, počáteční hustotu, počáteční obsah vlhkosti v hmotnostních procentech, tepelnou vodivost, dobu trvání požáru a vystavení požáru. Výsledky, tj. grafy rozložení teploty po průřezu desky, jsou zobrazeny na stejné stránce.
4. Nulový tok na nevystavené straně
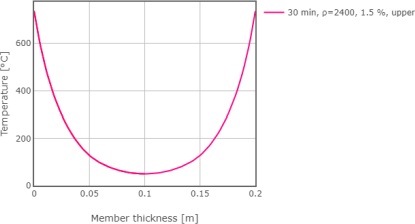
Obr. 2: Rozložení teplot v desce o celkové tloušťce 200 mm oboustranně vystavené požáru
V této kapitole je názorně demonstrováno, že problém desky oboustranně vystavené požáru (viz Obr. 2) lze modelovat jako desku poloviční tloušťky s nulovým tepelným tokem na jedné straně (viz Obr. 3), srovnej s Hertz (2012). Z Obr. 4 je zřejmé, že výsledky jsou shodné pro obě varianty. Výhodou modelování polovičního problému je snížení výpočetního času a větší přehlednost výsledků. Tento způsob modelování je pro jeho názronost dále využíván v tomto článku.
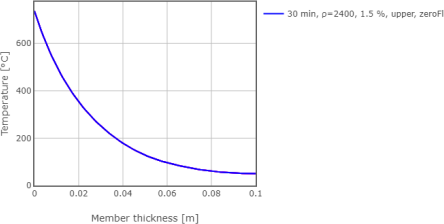
Obr. 3: Rozložení teplot v desce o celkové tloušťce 100 mm jednostranně vystavené požáru a jednostranně izolované
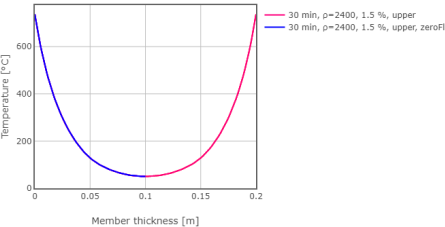
Obr. 4: Srovnání výsledků na Obr. 2 a 3
5. Porovnání s normovými grafy
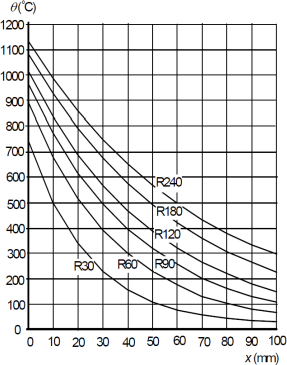
Obr. 5: Rozložení teplot dle (ČSN EN 1992-1-2 2006, Fig. A.2)
Druhý příklad je zaměřen na porovnání výsledků stanovených pomocí webové aplikace (Štefan & Holan 2020) (viz Obr. 6) a grafů uvedených v normě (ČSN EN 1992-1-2 2006) (viz Obr. 5). Vstupní parametry výpočtu jsou převzaty z (ČSN EN 1992-1-2 2006) – tj. tloušťka desky 200 mm, počáteční objemová hmotnost 2300 kg/m3, počáteční obsah vlhkosti 1,5 % a dolní limit tepelné vodivosti. Z Obr. 7 je zřejmé, že křivky rozložení teplot stanovení dle (ČSN EN 1992-1-2 2006) a (Štefan & Holan 2020) pro různé časy jsou shodné.
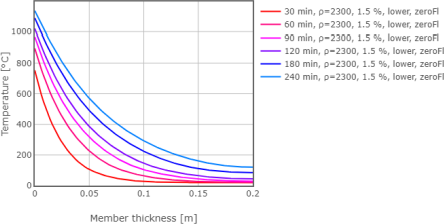
Obr. 6: Rozložení teplot dle webové aplikace (Štefan & Holan 2020)
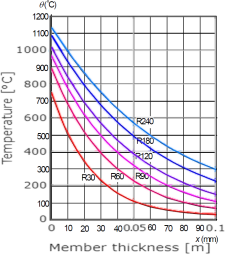
Obr. 7: Srovnání výsledků na Obr. 5 a 6
6. Parametrická studie
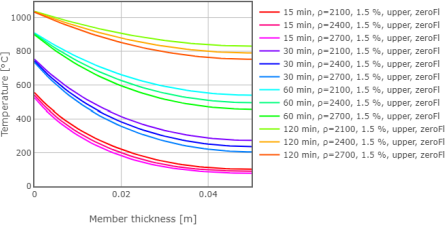
Obr. 8: Rozložení teplot v desce o celkové tloušťce 100 mm
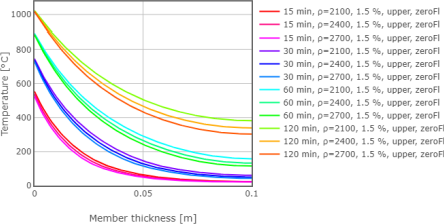
Obr. 9: Rozložení teplot v desce o celkové tloušťce 200 mm
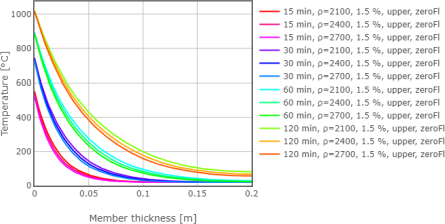
Obr. 10: Rozložení teplot v desce o celkové tloušťce 400 mm
V této kapitole je prezentována parametrická studie vlivu počáteční objemové hmotnosti na rozložení teploty po tloušťce betonové desky vystavené požáru na obou površích. Výpočty jsou provedeny pro celkové tloušťky desky 100 mm, 200 mm a 400 mm. Při výpočtech jsou uvažovány různé počáteční objemové hmotnosti, konkrétně hodnoty 2100 kg/m3, 2400 kg/m3 a 2700 kg/m3. Výpočty jsou provedeny pro dobu trvání požáru 15 minut, 30 minut, 60 minut a 120 minut. Počáteční obsah vlhkosti je uvažován jako 1,5 % hmotnosti betonu a pro tepelnou vodivost je uvažována horní mez dle ČSN EN 1992-1-2 (ČSN EN 1992-1-2 2006). Výsledky jsou zobrazeny na Obr. 8 až Obr. 10. Ze získaných výsledků lze vyvodit následující závěry. Na začátku požáru, kdy ještě není vnitřní část průřezu příliš zahřátá, je zřejmé, že objemová hmotnost má relativně velký vliv na teplotu v blízkosti povrchu. S rostoucím časem, a tedy se zvyšující se teplotou v desce, se zvyšuje vliv objemové hmotnosti na teplotu ve vnitřní části průřezu. S dalším zvýšením času a teploty se snižuje vliv objemové hmotnosti na teplotu v blízkosti povrchů a zvyšuje vliv objemové hmotnosti na teplotu v jádře.
7. Závěr
V článku byla prezentována autorem vytvořená webová aplikace pro stanovení rozložení teploty v betonové desce vystavené požáru. Webová aplikace, která vychází z algoritmu založeného na metodě konečných rozdílů a implementovaného v programovacím jazyce JavaScript, je uživatelsky přívětivá, snadno použitelná, lehce dostupná a rychlá. Dále bylo v článku prezentováno použití webové aplikace pro parametrickou studii zaměřenou na vliv počáteční objemové hmotnosti na rozložení teploty po průřezu desky. Závěrem parametrické studie je, že různé počáteční objemové hmotnosti ovlivňují na začátku požáru teplotu u povrchu desky a později ovlivňují teplotu ve vnitřní části průřezu. V rámci další práce bude aplikace rozšířena tak, aby bylo možné řešit komplexnější problémy – např. různé teplotní křivky, kombinace více materiálů, složitější geometrie a jiné.
Poděkování
Tato práce byla podpořena grantem Studentské grantové soutěže ČVUT č. SGS20/041/OHK1/1T/11.
Literatura
- Bažant, Z. P. & Jirásek, M. (2018), Creep and Hygrothermal Effects in Concrete Structures.
- Civil Calculation (2020), ‘Civil calculation’. URL: https://calculocivil.com/eu
- ČSN EN 1991-1-2 (2004), Eurokód 1: Zatížení konstrukcí – Část 1-2: Obecná zatížení – Zatížení konstrukcí vystavených účinkům požáru, ČNI.
- ČSN EN 1992-1-2 (2006), Eurokód 2: Navrhování betonových konstrukcí – Část 1-2: Obecná pravidla – Navrhování konstrukcí na účinky požáru, ČNI.
- EurocodeApplied.com (2020), ‘Eurocodeapplied.com’. URL: https://eurocodeapplied.com:443/
- Hertz, K. (2012), ‘Users guide for the program confire.exe’,
http://www.byg.dtu.dk/english/-/media/Institutter/Byg/publikationer/software/confire_users_guide_ver_2.ashx?la=da. Accessed: 2020-09-01. - Holan, J. & Štefan, R. (2019), ‘Numerická analýza rozložení teploty v betonové desce vystavené požáru pomocí webové aplikace’, 26. Betonářské dny 2019 Hradec Králové.
- using Eurocodes (2020), ‘using eurocodes’. URL: https://usingeurocodes.com/
- Štefan, R. (2015), Transport Processes in Concrete at High Temperatures. Mathematical Modelling and Engineering Applications with Focus on Concrete Spalling, PhD thesis, CTU in Prague.
- Štefan, R. & Holan, J. (2020), ‘Tedison’. URL: https://people.fsv.cvut.cz/~holanjak/software/tedison/
Článek se věnuje popisu softwarového stroje pro řešení problému vedení tepla v betonové desce vystavené požáru. Samotná metoda je založena na tzv. konečných prvcích, výpočet je integrován do webového rozhraní pomocí jazyka JavaScript. Samotná řešená úloha i použitá metoda je spíše standardní, inovativnost spočívá především v uživatelské přívětivosti a dostupnosti. Nástroj lze spustit na jakémkoliv zařízení i uvnitř jakéhokoliv OS, není třeba jej instalovat. Nástroj má potenciál výrazně snížit náročnost použití této metody v praxi, byť je omezen na specifickou úlohu. Článek doporučuji k vydání.
The paper presents a newly developed web application for the calculation of heat transfer over the thickness of a concrete slab during fire. The algorithm is based on the finite difference method and is implemented using the JavaScript programming language. The GUI for the input of calculation parameters and for the interpretation of the results is created using the HTML markup language. The paper also presents the theory behind the algorithm and examples of various problems solved using the web application. From the presented results, it is readily seen that the new web application is user-friendly, highly accessible, and very fast.