Statistické hodnocení zkušebních metod stanovení koncentračních mezí výbušnosti hořlavých plynů a par
Článek je svým obsahem určen zejména těm, kteří se zabývají zkušebním stanovením koncentračních mezí výbušnosti a těm, kteří budou připravovat revizi normy ČSN EN 1839-ed.2. Text vychází z dlouholeté teoretické a praktické zkušenosti autora a s odkazem na domácí a zahraniční odbornou literaturu. Základní úvahy k potřebnosti koncentračních mezí výbušnosti jsou nahlíženy i z hlediska statistiky, tedy možnosti určení pravděpodobnosti výbuchu při koncentracích dolní meze výbušnosti a horní meze výbušnosti a volby pravděpodobnostní funkce v závislosti na koncentraci hořlavých plynů nebo par hořlavých kapalin.
Úvod
Znalost dolní meze výbušnosti (dále jen DMV) a horní meze výbušnosti (dále jen HMV) má velký praktický význam při realizaci protipožárních a proti výbuchových opatření ve výrobě, skladování a užívání hořlavých plynů a hořlavých kapalin podle platných předpisů [1], [2], [3], [4], [5], [6], [7] a další. Koncentrační meze výbušnosti (dále jen KMV) jsou využívány při analýze rizik a následných škod metodami:
- kvalitativního (popisného) posouzení, hodnotící potenciální rizika, např.:
- HAZOP (Hazard and Operability Analysis–Analýza nebezpečí a provozuschopnosti) [8],
- What – if Analysis (Analýza toho, co se stane, když) [9],
- Check list Analysis (Analýza kontrolního seznamu) [10],
- FMEA (Failure Modes and Effects Analysis–Analýza způsobů a důsledků poruch) [11],
- kvantitativního (numerického) posouzení, které počítá pravděpodobnost výskytu nežádoucí události, např.:
- CPQRA (Chemical Process Quantitative Risk Analysis – Kvantitativní analýza rizika chemického procesu) [12].
- kombinovaného (relativního) hodnocení, kombinující kvalitativní a kvantitativní hodnocení, např.:
- DOW´s Fire and Explosion Index (Dowsův index výbuchu a požáru) [13],
- FTA (Fault Tree Analysis – Analýza stromu poruchových stavů) [14],
- IAEA TECDOC-727 (International Atomic Energy Agency TECDOC – Mezinárodní agentura atomové energie TECDOC – Metoda relativní priorizace rizik) [15],
- ETA (Event Tree Analysis – Analýza stromu události) [16].
Podrobný popis těchto metod k analýze rizik nežádoucích událostí vzniku výbušné atmosféry po úniku hořlavých plynů nebo par hořlavých kapalin včetně existujících počítačových nástrojů čtenář nalezne např. v uvedené literatuře.
Klíčovým cílem studií následků havárií jsou analýzy rozptylů k odhadu pozice, tvaru a velikosti výbušného oblaku, jehož velikost a tvar jsou definovány pomocí hodnot KMV. Aplikovaný program (SW) počítá izopletu DMV jako předpokládanou spojnici míst s touto výbušnou koncentrací v oblaku plynu. Dále jsou výpočetně odhadovány výbušná hmotnost oblaku na základě jeho hmotnosti s koncentracemi mezi DMV a HMV a z ní energie výbuchu a výsledný průběh tlakového rázu a impulzu (plocha pod křivkou tlak versus čas). Znalost hodnot KMV je dále využívána k nastavení parametrů elektrické požární signalizace (EPS) a havarijního větrání při havarijním úniku plynu nebo par [17].
Hodnoty DMV a HMV jsou výrobci/dodavateli hořlavých látek a jejich směsí uváděny v příslušných bezpečnostních datových listech mezi fyzikálními a chemickými vlastnostmi. Stanovují se zkušebně v akreditovaných laboratořích podle platných zkušebních norem. V ČR je to ČSN EN 1839- ed.2 [18], známé jsou dále ASTM E 681-09 [19], GOST 12.1.044-89 [20]. Mezinárodně uznávané zkušební normy jsou v tomto případě nezbytné, neboť hodnoty KMV jsou závislé na řadě faktorů: konstrukci zkušebního zařízení, teplotě, tlaku, složení testovaných látek, směru šíření plamene po iniciaci, iniciační energii, vlivu konvekce, turbulence a kritérií výbuchu [21], viz následující tab. č. 1.
| Zkušební metoda | Zkušební nádoba | Kritérium výbuchu |
|---|---|---|
| ČSN EN 1839-ed.2 metoda T | Skleněná vertikální trubice: průměr 8 cm±2 mm, délka 30 cm | Pohyb plamene vzhůru od jiskřiště do vzdálenosti ≥ 30 cm |
| ČSN EN 1839-ed.2 metoda B | Válcová nebo kulová nádoba z nerezu o objemu ≥ 5 dm3 | Nárůst tlaku 5 ±0,1 % poč. tlaku |
| ASTM E-681 | Skleněná kulová baňka o objemu 5 dm3 | Rozšíření plamene od zdroje vznícení vzhůru i do stran |
Rozdílnosti ve zkušebních metodách se projevují i v diferencích naměřených hodnot KMV, viz tab. č. 2.
| Zkušební metoda | DMV [% obj.] | HMV [% obj.] |
|---|---|---|
| ASTM E-681 | 5 | 15 |
| ČSN EN 1839-ed.2 metoda T | 4,4 ± 0,2 | 16,6 ± 0,2 |
| ČSN EN 1839-ed.2 metoda B | 4,6 ± 0,2 | 16,8 ± 0,2 |
Rozdíly mezi mezemi výbušnosti, stanovenými těmito metodami mohou být až 10 % relativní hodnoty.
Pochybnosti a nejistotu vyvolávají následující definice např. [18]:
Rozsah výbušnost (explosion range): Rozmezí koncentrace hořlavé látky nebo směsi látek ve vzduchu, ve kterém může dojít k výbuchu.
Dolní mez výbušnosti DMV (Lower Explosion Limit nebo Lower Flammability Limit): spodní hranice rozsahu výbušnosti, ve kterém může dojít k výbuchu.
Horní mez výbušnosti HMV (Upper Explosion Limit nebo Upper Flammability Limit): horní hranice rozsahu výbušnosti, ve kterém může dojít k výbuchu.
Poznámka v normě: KMV nejsou součástí rozsahu výbušnosti.
Pro statistický přístup tak vznikají následující otázky:
- jak lépe definovat KMV a výbuch ve zkušební komoře,
- určení pravděpodobnosti výbuchu při KMV a možnosti hodnocení přesnosti a správnosti [22], [23],
- volba pravděpodobnostní funkce [24],
- návrh uspořádání pokusu s cílem odhadu xp(DMV) a xp(HMV) podle výsledků série měření.
1. Základní úvahy k definici KMV a výbuchu
![Obr. 1 Schéma hypotetického průběhu pravděpodobnosti výbuchu P(x) v závislosti na koncentraci x [%] hořlavé látky ve směsi se vzduchem](/docu/clanky/0221/022193o1.png)
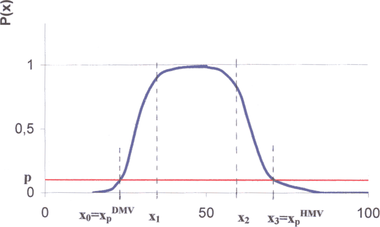
Obr. 1 Schéma hypotetického průběhu pravděpodobnosti výbuchu P(x) v závislosti na koncentraci x [%] hořlavé látky ve směsi se vzduchem
Ani v jedné z výše uvedených norem není jednoznačně uvedeno, že koncentrace pod DMV nebo nad DMV nejsou zcela jistě nevýbušné a v oblasti výbušnosti zcela jistě výbušné. Výše uvedené definice mohou asociovat představu podle obr. 1.
Tato představa je zjevně nesprávná, neboť je známo, jak jsou KMV a vlastní proces výbuchu závislé na řadě výše uvedených faktorů. S tím počítají i zkušební postupy, když sledují kolikrát výbuch při dané koncentraci proběhl a kolikrát nenastal.
Reálná je proto představa funkce P(x) jako pravděpodobnost výbuchu při koncentraci x, viz obr. 2. Na základě zkušeností z měření v laboratoři lze usuzovat, že v oblasti DMV křivka pravděpodobnosti poměrně prudce stoupá, viz interval (x0, x1) z obr. 2, dále že následuje interval, ve kterém je téměř konstantní s P = 1, viz interval (x1, x2) z obr. 2, zatímco v okolí HMV naopak prudce klesá, viz interval (x2, x3) z obr. 2, avšak mírněji, než stoupá v okolí DMV.
Je patrno, že pravděpodobnost výbuchu při koncentraci x = xp bude ve skutečných proměnných podmínkách vyšší, tj. křivka P(x) bude plošší (v dané hypotetické situaci). Je možné předpokládat, že stejné látce existuje několik (svazek) křivek P(x).
Při návrhu zkušební metody by proto měly být voleny zkušební podmínky, které jsou z hlediska bezpečnosti nejvíce nebezpečné.
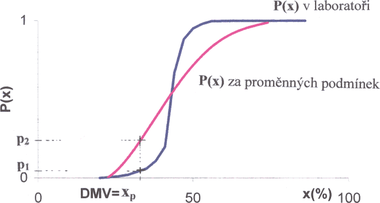
Obr. 3 Představa srovnání průběhu funkce P(x) v laboratoři a v reálných podmínkách při koncentracích x
Před návrhem určité pravděpodobnostní funkce P(x) je možné připustit, že její tvar bude jiný za relativně přísně definovaných podmínek v laboratorním zkušebním zařízení a jiný v neřízených, silně fluktujících podmínkách reálných situací. Tento vliv je zvažován v obr. 3.
Nabízí se tak možnost definovat DMV nebo HMV jako koncentraci hořlavé látky (plyn, pára), při které za definovaných podmínek nastane výbuch s určitou dohodnutou (oprávněnou) pravděpodobností a s určitým koeficientem spolehlivosti výsledku. Otázkou je, zda stanovit pravděpodobnost výbuchu např. 10−4 a jaké je riziko, že experimentálně naměřená hodnota odpovídá pravděpodobnosti jiné, např. 10−2. Pro zjednodušení dalších úvah předpokládejme, že podmínky zkoušek z hlediska zapalitelnosti výbušné směsi, indikace výbuchu a možnosti samovolného šíření plamene jsou jisté a že nevnášejí neurčitost, která by pro exaktní řešení musela být stanovena a zvážena.
2. Možnosti určení pravděpodobnosti výbuchu při koncentracích DMV a HMV, hodnocení přesnosti a správnosti
V technické praxi jsou běžné postupy, kdy se při určitých velikostech fyzikální veličiny x1 , x2 , …, xk uskuteční n1 , n2 , …, nk pokusů (ni ≥ 20) a zjišťuje se např. počet pozitivních výsledků ri , dosažení určité velikosti konverze reaktantu atp. Ze zjištěných hodnot (xi, ni, ri ), i = 1,2,…,k jsou následně vypočteny charakteristiky křivky P(x).
Problém stanovení KMV je obdobný, neboť jde o pravděpodobnost P(x), že zkoumaná látka bude při koncentraci x za určitých podmínek výbušná. Jsou zde však rozdíly: z technických/ekonomických důvodů není možné uskutečnit pro jednotlivé koncentrace xi (např. k = 8) počet zkoušek ni ≥ 20. To by znamenalo realizovat cca 160 zkoušek s velkým požadavkem na čas.
Problém je obtížnější vzhledem též k tomu, že nás zajímá pravděpodobnost při koncentraci cca x0,01, nebo x0,001 , a ne jenom x0,5 jako např. zdravotníky při zjišťování ED50 (účinná dávka léčiva) nebo LD50 (smrtelná dávka látky).
Při stanovení KMV je stanoven takový postup, že se zvyšuje nebo snižuje koncentrace x hořlavé látky (plynu, par) při malém počtu opakování pokusu (n = 3 nebo n = 5). Je proto obtížnější zkoumat statistické vlastnosti těchto pokusů, např. nyní moderní nejistotu měření. Umíme však vypočítat např.:
a) pravděpodobnost, že při koncentraci x, při které je pravděpodobnost výbuchu P(x) bude n pokusů za sebou bez výbuchu, viz následující tabulka č. 3.
| P(x) | n | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0,01 | 0,99 | 0,98 | 0,97 | 0,96 | 0,95 | 0,94 | 0,93 | 0,92 |
| 0,05 | 0,95 | 0,9025 | 0,86 | 0,81 | 0,77 | 0,73 | 0,698 | 0,66 |
| 0,1 | 0,9 | 0,81 | 0,73 | 0,66 | 0,59 | 0,53 | 0,48 | 0,43 |
| 0,2 | 0,8 | 0,64 | 0,51 | 0,41 | 0,33 | 0,26 | 0,21 | 0,17 |
| 0,3 | 0,7 | 0,49 | 0,34 | 0,24 | 0,17 | 0,12 | 0,08 | 0,58 |
| 0,5 | 0,5 | 0,25 | 0,125 | 0,06 | 0,03 | 0,015 | 0,0078 | 0,0039 |
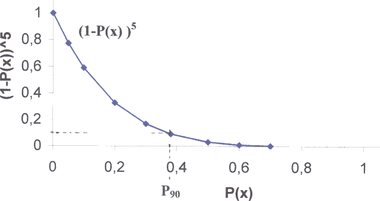
Názorně je tato závislost patrná z obr. č. 4 pro n = 5 nezávislých pokusů s koncentrací x. Číslo 0,38 je tzv. Horní mez spolehlivosti pro pravděpodobnost s koeficientem spolehlivosti 0,9 (též tzv. 90% horní mez spolehlivosti nebo 90% horní konfidenční mez).
b) pro libovolný počet pokusů n a libovolný koeficient spolehlivosti (1−α), mez spolehlivosti nebo naopak pro zvolenou hodnotu meze spolehlivosti a určitý počet pokusů koeficient spolehlivosti (1−α), viz následující tabulka 4.
| n | 1−α | |||
|---|---|---|---|---|
| 0,8 | 0,9 | 0,95 | 0,99 | |
| 1 | 0,8 | 0,9 | 0,95 | 0,99 |
| 2 | 0,447 | 0,684 | 0,776 | 0,90 |
| 3 | 0,415 | 0,535 | 0,611 | 0,785 |
| 4 | 0,331 | 0,438 | 0,527 | 0,684 |
| 5 | 0,275 | 0,369 | 0,451 | 0,602 |
| 10 | 0,149 | 0,250 | 0,259 | 0,369 |
| 15 | 0,102 | 0,142 | 0,181 | 0,264 |
| 20 | 0,077 | 0,109 | 0,181 | 0,206 |
Jestliže se tudíž uskuteční např. 5 pokusů bez výbuchu s určitou koncentrací, potom pravděpodobnost výbuchu může být < 0,451 při spolehlivosti 95 %, tj. s rizikem náhodného výbuchu 5 %. Pokud bychom považovali směs za výbušnou s P(x) ≥ P0 a s 95% spolehlivostí, museli bychom provádět n = log 0,05/log (1−P0) počet zkoušek, to jsou ovšem základy pravděpodobnosti. Pro další úvahy bude vhodné zavést funkci, která by vystihovala křivku P(x).
3. Volba pravděpodobnostní funkce v závislosti na koncentraci hořlavé látky
Jak již bylo uvedeno v části 1, je nezbytné z hlediska statistiky použít vhodnou funkci P(x), která by ke každé koncentraci x udávala pravděpodobnost, že látka ve výbušné směsi s plynným oxidantem bude po iniciaci reagovat výbušně. Nazvěme tuto funkci např. Statistická charakteristika výbušnosti (v elektrotechnice např. je používán pojem statistická charakteristika vypínacích obvodů) [25].
Laický názor podle obr. 1, že pro všechny koncentrace x < DMV a pro všechny x > HMV je výbuch zcela nemožný i za kontrolovaných podmínek v laboratoři, lze matematicky vyjádřit např. takto
Z hlediska statistiky je reálná představa dvou hodnot čísel xp(DMV) a xp(HMV) takových, že
když p je zdůvodnitelná hodnota (konvenční), např. 0,01 nebo 0,001 či 0,0001, viz obr. 2 výše. K řešení tohoto problému je však nutné zavést funkci P(x) s malým počtem parametrů. Obrázek č. 2 nabízí tyto možnosti:
a) pro vzestupnou část
kde F je zvolená rostoucí funkce a μ(DMV) a σ(DMV) jsou její parametry, které jsou závislé na látce a podmínkách zkoušky.
Doporučuje se ověřit praktickou užitečnost např. funkce
což je distribuční funkce normovaného normálního rozdělení se střední hodnotou 0 a směrodatnou odchylkou 1. Funkce Φ(u) je tabelována, takže její výpočet je pohodlný.
b) pro sestupnou část
kde F je daná rostoucí funkce a μ(HMV) a σ(HMV) jsou její parametry.
Následující tabulka č. 5 je příkladem výpočtu, numerickým pokusem s tímto zadáním:
Φ(u), viz rovnice (5)
- μ(DMV) = 2 %, σ(DMV) = 0,5 %
- μ(HMV) = 10 %, σ(HMV) = 4 %
| x [%] | P(x) |
|---|---|
| 0,5 | 0,001350 |
| 1 | 0,0227 |
| 1,5 | 0,1587 |
| 2 | 0,5 |
| 3 | 0,9773 |
| 4 | 0,9999 |
| 6 | 0,8413 |
| 8 | 0,6915 |
| 10 | 0,5 |
| 12 | 0,3085 |
| 14 | 0,1587 |
| 16 | 0,0668 |
| 20 | 0,0062 |
Je patrné, že numerické hodnoty P vystihují předpokládaný průběh podle obr. 2.
Zřejmě lze odvodit více typů (tvarů) křivek, funkcí P(x), které by opět mohly být numericky testovány a vzájemně porovnávány.
Rovnice č. 7 a 8 lze sečíst do jedné funkce vystihující vzestupnou i sestupnou část.
4. Návrh uspořádání pokusu
Při poslední sérii pokusů máme podle zkušebního postupu při určité koncentraci x = a sérii n pokusů „bez výbuchu“ a při určité vyšší koncentraci x = b = a + Δ, sérii n pokusů alespoň s jedním „výbuchem“, který může nastat při r-tém pokusu.
Je důležitá otázka, jak odhadnout pravděpodobnosti P(x = a) a P(x = b) a zda by vyhověl odhad pravděpodobnosti výbuchu,
- při koncentraci x = a, když při ní výbuch nenastal ani v jednom z n pokusů, pomocí rovnice
Pa,odhad(x = a) ≅ 1/(n + 2) (9)
- při koncentraci x = b, když při n pokusech výbuch nastane pouze v r-tém pokusu, pomocí rovnice
Pb,odhad (x = b) ≅ 2/(r + 2)r = 1,2, …………, n (10)
Pokud by bylo reálné pomocí rovnic č. 9 a 10 odhadnout pravděpodobnosti při koncentracích x = a, x = b, lze odhadnout konstanty μ a σ u rovnic č. 7 a 8.
Jsou-li dále k dispozici odhady parametrů μ a σ, lze pro libovolnou koncentraci x odhadnout pravděpodobnost Podhad(x) z rovnice
Závěr
Ze základních úvah a experimentů podložených domácí i zahraniční literaturou vyplývá potřebnost revize ČSN EN 1839-ed.2, a to zejména v oblasti zkušebního stanovení koncentračních mezí výbušnosti. Jeví se zde reálná možnost pro to, aby bylo možné pro určitý počet pokusů, např. 3 nebo 5, se znalostí experimentálně stanovených koncentrací a (při n pokusech bez výbuchu) a b (při r-tém pokusu s prvním výbuchem) vypočítat např. x0,01 nebo x0,001, tj. koncentrací s 1% pravděpodobností nebo 0,1% pravděpodobností výbuchu, respekt. s pravděpodobností, kterou by zkušební norma taxativně stanovovala, a to jak při stanovení DMV, tak i HMV.
Dále by bylo vhodné upřesnit/doplnit/zvážit např. v normě [18] při její revizi:
- v tab. 1 termín „Maximální nejistota měření“ zkoušené látky ve zkušební směsi nahradit normalizovanou „standardní kombinovanou nejistotou“ (combined standard uncertainty) nebo „rozšířenou nejistotou“ (expanded uncertainty) [26],
- v příl. E doplnit do zkušebního protokolu kromě P(DMV) a P(HMV) též „rozšířenou nejistotu“ výsledku zkoušky s koeficientem pokrytí (coverage factor) k = 2,
- v příl. F doplnit „mez opakovatelnosti r“ (repeatability limit) a „mez reprodukovatelnosti R“ (reproducibility limit).
Literatura
- Zák. č. 350/2011 Sb., o chemických látkách a chemických směsích a o změně některých zákonů.
- Nařízení komise EU č. 830/2015 o registraci, hodnocení, povolování a omezování chemických látek.
- Zák. č. 224/2015 Sb., o prevenci závažných havárií způsobených nebezpečnými chemickými látkami nebo chemickými směsmi…
- NV č. 116/2016 Sb., o posuzování shody zařízení a ochranných systémů určených k použití v prostředí s nebezpečím výbuchu při jejich dodávání na trh.
- Vyhl. č. 402/2011 Sb., o hodnocení nebezpečných vlastností chemických látek a chemických směsí a balení a označování
- Zák. č. 88/2016 Sb., kterým se upravují další požadavky BOZP při práci v pracovněprávních vztazích a zajištění BOZP nebo poskytování služeb mimo prac. vztahy…
- Zák. č. 133/1985 Sb., o požární ochraně.
- ČSN IEC 61882:2017 Studie nebezpečí a provozuschopnosti – Pokyn k použití.
- https://www.praxiom.com/risk-assessment.htm.
- https://managementmania.com/cs/analyza-kontrolni-seznam-cla-checklist-analysis.
- ČSN EN IEC 60812-ed.2:2019 Analýza způsobů a důsledků poruch.
- https://www.lehigh.edu/~intribos/Resources/SAE_FMEA.pdf.
- https://core.ac.uk/download/pdf/4271116.pdf.
- ČSN EN 61025:2007 Analýza stromu poruchových stavů
- https://www-pub.iaea.org/MTCD/publications/PDF/te_727r1_web.pdf.
- ČSN EN 62502:2011 Techniky analýzy spolehlivosti – Analýza stromu události.
- ČSN EN 50402 – ed. 2:2018 Elektrická zařízení pro detekci a měření hořlavých a toxických plynů nebo par nebo kyslíku-Požadavky na funkční bezpečnost systémů detekce plynů.
- ČSN EN 1839 ed. 2:2017 Stanovení mezí výbušnosti plynů a par.
- ASTM E 681-09: 2015 Standard test method for concentration limits of Flammability of Chemicals (vapours and gases).
- GOST 12.1 044 - 89: Occupational safety standard systém. Fire and explosion hazard of substances and materials. Nomenclature and methods of their determination.
- Dvořák, O. Užitný vzor Zkušební zařízení ke stanovení koncentračních mezí výbušnosti, maximálního výbuchového tlaku a brisance hořlavých plynů a par za technologických podmínek, č. Přihl.: 2014-29041, č. Zápisu: 26809.
- ČSN ISO 3534-1:2010 Statistika – Slovník a značky. Část 1: Obecné statistické termíny a termíny používané v pravděpodobnosti.
- ČSN ISO 5725-2:1997 Přesnost (správnost a shodnost) metod a výsledků měření – Část 2: Základní metoda pro stanovení opakovatelnosti a reprodukovatelnosti normalizované metody měření.
- ČSN ISO 3534-2:2010 Statistika – Slovník a značky – Část 2: Aplikovaná statistika.
- Dvořák, O. Problematika stanovení koncentračních mezí výbušnosti hořlavých plynů a par hořlavých kapalin. Disertační práce, VŠB-TUO, 1999.
- DVOŘÁK, O. The Uncertainty in Measurements of Flash Point. Joint Working Group of the ISO/TC 28, TC 35, CEN/TC 19 and TC 139, New Orleans, 1998.
Článek se zabývá aktuální tématikou vyhodnocení nejistot pokusných dat z měření koncentračních mezí výbušnosti. Vychází ze současného stavu problematiky ukotveného v normách pro laboratorní stanovení koncentračních mezí výbušnosti. Zobecňuje současnou představu o koncentračních mezích výbušnosti jako přesných hodnot koncentrací a analyzuje případ opakovaných stanovení HMV nebo DMV a interpretaci pozorovaného počtu pozitivních a negativních výsledků měření. Navrhuje nahradit diskrétní hodnoty mezí výbušnosti funkcí, která má pro meze výbušnosti hodnotu 0,5, uvnitř rozmezí výbušnosti hodnotu 1 a směrem ven z rozmezí výbušnosti klesá k nule. Tato možnost se jeví jako reálná. Článek tak přináší nový pohled na pojetí koncentračních mezí výbušnosti. Doporučuji k publikaci.
Basic considerations on the need for the LFL and UFL and in terms of statistics on the definition of Flammability concentration limits and explosion criteria according to ČSN EN 1839-ed.2, as well as the possibility of determining the probability of explosion at the Flammability limits concentrations and the choice of a probability function depending on the concentration of flammable gases and liquids vapours. The content of the article is intended especially for those who are engaged in the test determination of flammability limits and those who will be preparing a revision of this standard. The text of the article is based on many years of theoretical and practical experience of the author and with reference to the expert literature.