Navrhování prostorových přípojů dřevostaveb za pomoci kování

1 Úvod

Obr. 1: Prostorový přípoj za pomoci úhelníku

Prostorové přípoje dřevostaveb za pomoci tenkostěnných ocelových elementů, aneb kování, pozvolna vytěsňují tradiční tesařské přípoje. Jejich hlavní výhodou je, že neoslabují průřezy spojovaných dřevěných prvků. Dalšími výhodami jsou možnost jejich provádění přímo na stavbě a možnost přímého napojení dřevěných prvků na ocelové či betonové konstrukce.

Jedním z nejpoužívanějších prvků pro přípoje za pomoci kování jsou tenkostěnné ocelové úhelníky. Viz obr. 1.

2 Chování prostorových přípojů za pomoci kování

Pro přípoje za pomoci kování dřevěných konstrukcí, je typická značná poddajnost. Ta způsobuje před dosažením únosnosti spoje velké plastické deformace. Toto chování je velice příznivé, protože lze pouhým okem rozpoznat přetížené spoje a včas podniknout kroky k zamezení hrozícího kolapsu nosné konstrukce. Únosnost spojů s kováním vychází ze tří možných způsobů jejich porušení. Jsou jimi: selhání oceli kování v oslabeném průřezu, roztržení připojovaného dřevěného prvku a dosažení únosnosti skupiny spojovacích prostředků.

3 Současná podpora v normách a odborné literatuře

Eurokódy [1] [2] [3] neřeší problematiku navrhování spojů s použitím kování komplexně, nicméně některé jeho části se této problematiky přímo dotýkají. Únosnost ocelového plechu kování, lze v souladu s Eurokódem 3 [2], spočítat jako by se jednalo o skořepinu, tj. poměrně náročným výpočtem. Hodnoty únosnosti ocelového plechu kování však obvykle vypočítávají přímo výrobci a kování bývá navrženo tak, aby pro únosnost spoje nebyla únosnost ocelového plechu rozhodující. Eurokód 5 [1] dále řeší výpočet únosnosti dřevěného prvku na tah kolmo k vláknům. Ač se ze své podstaty jedná o únosnost dřevěného prvku, tento posudek bývá součástí posouzení spoje jakožto celku a je vždy potřeba se jím zabývat. Eurokód 5 [1] dále obsahuje tabulku minimálních přípustných roztečí a vzdáleností od okrajů pro hřebíky. Přenásobením hodnot součinitelem 0,7 pro spoj ocelová deska-dřevo lze jednoznačně definovat oblast spoje, do které lze tenkostěnné ocelové elementy umístit. U roztečí však mnoho výrobců minimální hodnoty z Eurokódu 5 [1] nerespektuje. Rastr otvorů pro hřebíky navíc bývá kvůli prolisům a otvorům pro svorníky nepravidelný, což ještě více znesnadňuje aplikaci pravidel. Proto bývá pravidlo o minimálních roztečích pro hřebíky převedeno na pravidlo o minimální ploše na hřebík, čemuž se hlouběji věnuje STEP1 [4].

STEP1 [4] je první z řady publikací vytvořených v rámci programu Structural Timber Education Programme a je v podstatě jistým komentářem k navrhování dřevěných konstrukcí podle Eurokódů. Problematikou navrhování spojů s použitím kování se věnuje část C13: Spoje s tvarovými součástmi z ocelového plechu. V ní je uveden příklad výpočtu únosnosti patky nosníku, takzvané U-botky, spolu s informacemi ohledně nosného působení přípojů dřevěných konstrukcí pomocí kování.

Technický předpis č. 17 (TR-Technical Report) [5] vydaný organizací EOTA obsahuje vzorový příklad výpočtu únosnosti úhelníku během namáhání na jeho rozevření. Jedná se o takzvaný výpočet shora, kdy je nejprve spočítána únosnost celé soustavy a až poté jsou kontrolovány jednotlivé podmínky rovnováhy, které výslednou hodnotu mohou redukovat. Únosnost je určena na základě úvahy, že v úhelníku vzniknou dva liniové plastické klouby, mezi kterými je skupina hřebíků namáhána na vytažení. Vyjádřeno rovnicí:

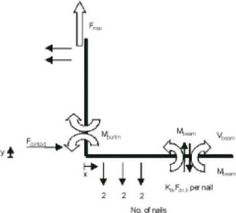
Obr. 2: Statické schéma výpočtu dle TR 17

kde je

F_max

– maximální síla na úhelník

M_purlin,k

– momentová únosnost rohu úhelníku

M_beam,k

–  momentová únosnost v rameni úhelníku

k_ax

– součinitel efektivity

F_ax,k

– pevnost na vytažení jednoho hřebíku

n

– počet efektivních hřebíků

x_y

– poloha plastického kloubu

Σx

– součet souřadnic hřebíků

Omezující podmínka, která ověřuje, zda jsou hřebíky schopny přenést zatížení při vzniku plastických kloubů:

V případě, že vyjde záporná hodnota, je zřejmé, že hřebíky nejsou schopny přenést zatížení a statický model je změněn na jiný, kde je předpokládáno, že momentová únosnost úhelníku je schopna přenést zatížení od efektivního počtu hřebíků namáhaných na vytažení.

Přístup dle EOTA TR 17 je nejen značně zjednodušen, ale je i velice obtížně použitelný. První významné zjednodušení je, že plastické klouby jsou uvažovány jako lineární, přičemž je experimentálně dokázáno, že v půdorysu jdou cestou nejmenšího odporu. Plastická únosnost se tedy může značně lišit od hodnoty, kterou výpočet uvažuje. Dalším zjednodušením je, že u hřebíků není uvažováno sekundární zpevnění vlivem páčení. Hřebíky tedy mají citelně vyšší únosnost, než je ve výpočtu uvažováno. A nejpodstatnějším zjednodušením je, že je zanedbán vliv tlačeného konce úhelníku, který je relativně velký a navíc je na nebezpečné straně výpočtu.

Tlačený konec úhelníku totiž vyvolává páčící posouvající sílu, která působí v opačném směru než vytahované hřebíky a tím snižuje výslednou vypočítanou hodnotu únosnosti.

Důvodem, proč je výpočet podle EOTA TR 17 jen obtížně použitelný, jsou výpočtem nezjistitelné vstupní údaje. Momenty vyvolávající plastické klouby jsou v příkladu určeny experimentálně. Únosnosti hřebíků na vytažení nejsou určeny v souladu s Eurokódy, ale podle dánských norem. A navíc počet hřebíků (3 řady) plně namáhaných na vytažení je určen bez bližšího vysvětlení, což je dokonce v rozporu s jinou větou předpisu, kde je zakázáno plně uvažovat více jak dvě řady hřebíků namáhaných na vytažení.

Z těchto důvodů bylo přistoupeno k rozvinutí tohoto výpočtu tak, aby byl snáze použitelný a více odpovídal reálnému působení zatížených úhelníků.

Obr. 3: Numerický model úhelníku

4 Výzkum na ČVUT v Praze

Výzkum probíhá ve spolupráci se společnostmi BOVA Březnice a FINE s.r.o. Jedná se tedy o, v současnosti značně ceněný, aplikovaný výzkum při spolupráci vědecké instituce s praxí. Základní části výzkumu jsou dále v textu představeny na příkladu výše zmíněného postupu optimalizace návrhu úhelníků zatížených na otevření.

Optimalizace na prostorových numerických modelech

K nalezení optimální pozice hřebíků v úhelníku a tvaru prolisu bylo využito numerických modelů v programu Abaqus CAE. Plechy úhelníků byly podrobeny elasto-plastické analýze. Připojované prvky tvořily pružné podložení ramen úhelníků. A hřebíky odolávaly tahu pružně. Ač se jednalo o relativně zjednodušený model, přesnost výsledků byla dostačující.

Experimenty

Experimenty byly provedeny dle EOTA TR 16 [6] a byla z nich určena experimentální charakteristická hodnota únosnosti. Jednotlivé únosnosti přípojů byly určeny na základě dvou limitů: porušení vzorku nebo maximálního přetvoření 15 mm. Experimenty byly prováděny na souborech 10 vzorků, aby výsledná únosnost vycházela z vyššího kvantilu, než u minimálního přípustného počtu vzorků, který je roven pěti. Výsledné charakteristické únosnosti byly určeny dle Eurokódu 0 [3]. Převod na únosnost pro obecné dřevo C24 proběhl dle EOTA TR 16 [6].

Obr. 4: Deformace úhelníku při kolapsu přípoje

5 Závěr

Ačkoliv na trhu existuje pestrý výběr kování a jeho obliba použití na spoje dřevěných konstrukcí vzrůstá, jeho normativní podpora není dostatečná. V odborné literatuře lze při zevrubné studii nalézt značné množství informací týkající se této problematiky, chybí však jejich ucelený přehled a v některých případech je i potřeba je revidovat. Na odstranění tohoto problému se však již pracuje na Univerzitním centru energeticky efektivních budov ve spolupráci s firmami BOVA a FINE.

Aktuálně je potřeba revidovat technický předpis EOTA TR 17 [5], u kterého byly s pomocí experimentálně ověřených hodnot zjištěny významné nedostatky. Jeho revize již je ve fázi certifikace CE.

Poděkování

Experimentální výzkum byl podpořen grantem SGS13/171/OHK1/3T/11.

Analýza problematiky a tento článek vznikly za podpory Evropské unie, projektu OP VaVpI č. CZ.1.05/2.1.00/03.0091 – Univerzitní centrum energeticky efektivních budov.

Zvláštní poděkování také patří firmě BOVA Březnice spol. s.r.o. za poskytnutí trojrozměrného vektorového modelu vyráběného kování použitém v obrázku č. 1 v tomto příspěvku.

Odkazy

• [1] ČSN EN 1995-1-1 Navrhování dřevěných konstrukcí – Část 1-1: Obecná pravidla – Společná pravidla a pravidla pro pozemní stavby, ČNI, Praha, 2006.
• [2] ČSN EN 1993-1-1 Navrhování ocelových konstrukcí, Část 1-1 Obecná pravidla a pravidla pro pozemní stavby, ČNI, Praha, 2006
• [3] ČSN EN 1990 ed.2 Eurokód: Zásady navrhování konstrukcí, ÚNMZ, 2011
• [4] Koželouh, B. Dřevěné konstrukce podle Eurokódu 5 – STEP1. Zlín: KODR, 1998. ISBN 80-238-2620-4.
• [5] EOTA TR 17: Worked example calculation of characteristic load-carrying capacities of 90° angle bracket with a rib. TECHNICAL REPORT 17, EUROPEAN ORGANISATION FOR TECHNICAL APPROVALS, Edition February 2002, Amended October 2012
• [6] EOTA TR 16: Method of testing Three-Dimensional Nailing Plates with examples. TECHNICAL REPORT 16, EUROPEAN ORGANISATION FOR TECHNICAL APPROVALS, Edition February 2002, Amended October 2012