prof. Ing. Josef Macháček, DrSc.

Recenzovaný V článku je uveden návrh předpjatých lanových sítí pro skleněné fasády v programu ANSYS. Po validaci navrženého modelu na publikovaných experimentech a verifikaci podle modelu v jiném publikovaném softwaru je použit pro parametrickou studii fasád s bodovými držáky („pavouky“). Studie zahrnuje dva rozměry sítě, spektrum jednopramenných nerezových lan Macalloy a laminované skleněné tabule různých tlouštěk. Předpětí lan bylo voleno jako 30 % jejich návrhové únosnosti podle publikovaných doporučení. Návrh respektuje platné evropské normy pro sklo a zatížení v mezních stavech použitelnosti i únosnosti. Výsledkem jsou tabulky uvádějící průhyby, napětí ve skle a síly v lanech sítě.

Recenzovaný Článek uvádí úvodní informace k návrhu předpjatých lanových sítí podpírajících rozměrné skleněné fasády. Popsány jsou jednotlivé fasádní prvky a příklady významných realizovaných fasád. V přehledu primárních publikací je ukázán vývoj experimentálních a teoretických přístupů k řešení problémů spojených s návrhem těchto konstrukcí (zajištění potřebné tuhosti a únosnosti, rizika spojená se selháním spojení skleněných tabulí s lanovou sítí, kolapsem kotev či ztrátou předpětí lan, dynamické chování při poruchách, výbuších a zemětřesení, vlivy teploty). Podrobněji jsou popsány práce použité v navazující části [31] pro validaci a verifikaci vlastního numerického řešení a parametrické studie těchto fasád.

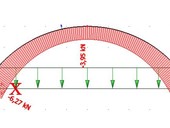
Recenzovaný V Části 2 jsou uvedeny vzpěrné délky týkající se oblouků trojkloubových, a to jak s vrcholovým kloubem vidlicovým (pouze v rovině oblouku), tak i trojkloubových oblouků s vrcholovým kloubem úplným (v rovině i z roviny oblouku). Článek navazuje na Část 1 [1], která zahrnuje oblouky dvojkloubové a vetknuté. Všechny studie jsou provedeny pro tři typy rovnoměrného zatížení (svislé po délce oblouku, svislé na půdorys oblouku a zatížení radiální). Hodnoty vzpěrných délek ekvivalentního přímého (Eulerova) prutu s konstantní osovou silou odpovídající maximální osové síle v patce oblouků jsou uvedeny ve formě grafů pro uzavřené trubkové průřezy, pro různé otevřené válcované průřezy IPE a různé širokopřírubové průřezy HEB.

Recenzovaný Uvedeny jsou výsledky rozsáhlé studie týkající se vzpěrných délek kruhových ocelových oblouků. Studie v Části 1 pokrývá oblouky dvojkloubové a vetknuté, v Části 2 oblouky trojkloubové s vrcholovým kloubem vidlicovým (pouze v rovině oblouku) a trojkloubové oblouky s vrcholovým kloubem úplným (v rovině i z roviny oblouku). Všechny studie jsou provedeny pro tři typy rovnoměrného zatížení (svislé po délce oblouku, svislé na půdorys oblouku a zatížení radiální). Hodnoty vzpěrných délek ekvivalentního přímého (Eulerova) prutu s konstantní osovou silou odpovídající maximální osové síle v patce oblouků jsou uvedeny ve formě grafů pro uzavřené trubkové průřezy, pro různé otevřené válcované průřezy IPE a různé širokopřírubové průřezy HEB. Studie navazuje na článek autora Stabilita ocelových kruhových oblouků [1], obsahující úvodní stabilitní analýzu dvojkloubových oblouků.

Recenzovaný V textu je parametricky vyšetřována stabilita a vybočení podpěrných oblouků válcové membránové konstrukce pomocí lineární bifurkační analýzy. Pro široké spektrum praktických geometrických parametrů konstrukce, předpětí membrán, způsobů uložení oblouků i čel membrány jsou uvedeny součinitele vzpěrných délek pro vybočení v rovině i z roviny oblouků a porovnány se stejnými součiniteli samostatných oblouků. Článek navazuje na Část 1: Experimenty a analýza [1], kde je uveden numerický model v programu SOFiSTiK a jeho validace pro membránové konstrukce podepřené ocelovými oblouky.

Recenzovaný V článku se popisuje a analyzuje test modelu přístřešku s textilní membránou podpíraného trubkovým ocelovým obloukem. Cílem vyšetřování je prostorové chování podpěrného oblouku pro jeho návrh z hlediska stability. Testuje se rozdíl chování samostatného vetknutého oblouku oproti jeho chování v membránové konstrukci. Uvedena jsou vstupní data, postup předpínání a zatěžování a experimentální výsledky. Pro numerickou analýzu v programu SOFiSTiK byla použita pružnostní, geometricky nelineární analýza s imperfekcemi respektující ortotropní chování membrány. Úspěšná validace numerických výsledků podle testů umožňuje rozsáhlé numerické parametrické studie zaměřené na stabilitu oblouků válcových membránových konstrukcí v druhé části článku.

Recenzovaný Článek analyzuje stabilitu dvojkloubových kruhových oblouků pro různá rovnoměrná zatížení (svislá na půdorys oblouku, svislá na délku oblouku a radiální na osu oblouku). Ke stanovení kritického zatížení se používá lineární bifurkační analýza a následně jsou určeny součinitele vzpěrné délky oblouků. S výjimkou radiálního zatížení je nutné vzhledem k proměnné normálové síle v obloucích uvažovat vztažný Eulerův základní prut se stejným průběhem proměnné osové síly. Analýza byla provedena pro různé okrajové podmínky oblouků v podporách. Studie zahrnovala oblouky s uzavřenými i otevřenými průřezy a prokázala významný vliv tvaru průřezu na vzpěrné délky pro vybočení z roviny oblouků. Výsledkem jsou tabulky pro korektní součinitele vzpěrných délek.

Recenzovaný Článek navazuje na předchozí pojednání o předpjatých ocelových trubkách pouze s jedním křížem (Macháček a Píchal [13]). Vyšetřováno je vzpínadlo se dvěma kříži, zatímco ostatní parametry jsou shodné s testovaným a analyzovaným vzpínadlem s jedním centrálním křížem. Pro kritické zatížení a rozhodující tvary při vybočení nepředpjatého vzpínadla se uvádí lineární bifurkace. Pro předpjaté vzpínadlo je odvozeno analytické řešení, umožňující stanovit kritické zatížení pro libovolné předpětí, včetně optimálního předpětí ke stanovení maximální kritické síly. Hlavní studie uvádí geometricky, popř. i materiálově nelineární řešení s imperfekcemi v prostředí ANSYS. Ukazuje potřebu nelineárního řešení i pro stanovení kritického zatížení "ideálního" vzpínadla, zatímco pro stanovení únosnosti "imperfektního" vzpínadla, s příslušným počátečním průhybem, je zcela nezbytné. V závěru je analyzován vliv materiálové nelinearity i počtu křížů, s doporučeními pro návrh vzpínadel.

Recenzovaný Tento článek je zaměřen na experimenty se vzpínadly, numerické analýzy a jejich vyhodnocení. V teoretické části je uvedena lineární bifurkace (2D LBA) ke stanovení kritických sil a tvarů vybočení, geometricky nelineární analýza ke stanovení únosnosti imperfektních vzpínadel (3D GNIA) a geometricky a materiálově nelineární analýza ke stanovení únosnosti imperfektních vzpínadel z nerezových ocelí (3D GMNIA). Numerické výpočty jsou provedeny v softwaru ANSYS a validovány na experimentech. Parametricky jsou vyšetřeny vlivy počátečních průhybů, směru vybočení, materiálové nelinearity a způsobu uložení táhel na středovém kříži. Výsledky jsou shrnuty v praktická doporučení. Článek navazuje na předchozí obecné pojednání o předpjatých ocelových tlačených trubkách s jedním křížem (Macháček [1]).

Recenzovaný Článek se zabývá návrhem velmi štíhlých tlačených ocelových prvků. Návrhová únosnost běžných štíhlých tlačených sloupů je dána jejich vzpěrnou únosností, která je při velké štíhlosti malá. Modifikací štíhlého sloupu do vzpínadlového předpjatého systému vede k násobnému zvýšení návrhové únosnosti. V článku jsou popsány předpjaté vzpínadlové ocelové tlačené trubky s jedním křížem. Uvádějí se vztahy pro stanovení kritického zatížení „ideálního vzpínadlového prutu“ a dále vztahy pro určení maximální únosnosti „imperfektního vzpínadlového prutu“. Maximální únosnosti po redukci součinitelem materiálu vedou ke stanovení návrhové únosnosti v souladu s Eurokódem 1993-1-1. V závěru je uveden příklad výpočtu a porovnání únosností předpjatého (vzpínadlového) a nepředpjatého (běžného) prutu velké štíhlosti.