Tepelná a mechanická zatížení konstrukcí při požáru
Stanovení rozvoje požáru v požárním úseku s následným zjištěním teploty v jednotlivých částech konstrukce vyžaduje znalost mnoha parametrů. Nejdůležitějším krokem je stanovení návrhového požárního scénáře, který nejlépe odpovídá mimořádné požární situaci. Na základě návrhového požáru lze popsat průběh teplot v požárním úseku a určit přestup tepla do konstrukce. Podívejme se na několik modelů a na tepelná a mechanická zatížení konstrukcí.
Tepelná a mechanická zatížení konstrukcí při požární situaci lze určit podle ČSN EN 1991-1-2. Tato norma přejímá evropskou normu EN 1991-1-2:2002 Eurokód 1: Zatížení konstrukcí – Část 1-2: Obecná zatížení – Zatížení konstrukcí vystavených účinkům požáru. ČSN EN 1991-1-2 se musí pro stavby umístěné na území České republiky používat s národní přílohou NA, která obsahuje údaje platné pro území ČR. Pro navrhování konstrukcí na účinky požáru se použije společně s částmi EN 1992 až EN 1996 a EN 1999. Vzhledem k tomu, že se EN 1991-1-2 zabývá stanovením požárního zatížení konstrukcí vystavených účinkům požáru dělení stavby do požárních úseků, mezní rozměry požárních úseků, stanovení stupňů požární bezpečnosti, stanovení mezních délek, kapacit a typů únikových cest, zajištění podmínek k provedení požárního zásahu, instalace požárně bezpečnostních zařízení a specifické požadavky na jednotlivé druhy staveb jsou pak řešeny v národních technických předpisech.
Tepelné zatížení
Stanovení rozvoje požáru v požárním úseku s následným zjištěním teploty v jednotlivých částech konstrukce vyžaduje znalost mnoha parametrů. Nejdůležitějším krokem je stanovení návrhového požárního scénáře, který nejlépe odpovídá mimořádné požární situaci. Na základě návrhového požáru lze popsat průběh teplot v požárním úseku a určit přestup tepla do konstrukce. Tepelné zatížení, jemuž je konstrukce při požáru vystavena, je dáno čistým tepelným tokem ḣ net [W/m2] dopadajícím na povrch prvku. Čistý tepelný tok je způsoben prouděním a sáláním horkých plynů, plamenů nebo horkých povrchů konstrukcí. Důležitou úlohu při přestupu tepla představují součinitel emisivity povrchů a součinitel přestupu tepla prouděním. Podle EN1991-1-2 kap. 3 jej lze stanovit jako
kde
- ḣ net,c
- je složka čistého konvekčního tepelného toku,
- ḣ net,r
- je složka čistého sálavého tepelného toku.
Složka čistého konvekčního tepelného toku se stanoví podle:
Složka čistého sálavého tepelného toku se stanoví podle:
Základem rovnice pro čistý přenos tepla sáláním je Stephan-Boltzmannův zákon o sálání. Podle tohoto zákona určuje „teplota sálání z plamenů“ maximální sálání do ocelového prvku. Konzervativně může být tato teplota brána jako teplota plynu. Ta může být určena na základě modelu požáru. V rovnici čistého sálavého tepelného toku hrají roli následující fyzikální veličiny:
- Stephan-Boltzmannova konstanta (σ = 5,67 × 10−8 W/m2K4); fyzikální konstanta,
- povrchová emisivita prvku (εm); závisí na povrchovém materiálu,
- emisivita požáru (εf),
- polohový faktor (Φ); geometrická konstanta.
Čistý přenos tepla prouděním může být přibližně uvažován jako rozdíl teplot (θg − θm) a je charakterizován součinitelem přestupu tepla prouděním αc. V praxi se pohybuje od 25 (nominální požár) do 50 W/m2K (uhlovodíkové hoření).
Modely požáru
ČSN EN 1991-1-2 uvádí různé přístupy pro stanovení tepelného zatížení – normativní přístup, který používá pro stanovení tepelného zatížení nominální požár a přístup vycházející z vlastností využívající fyzikální a chemické parametry. Modely pro fyzikálně podložená tepelná zatížení lze nalézt v přílohách A, C a D. Rozložení teplot v požárním úseku při plně rozvinutém požáru lze předpovědět několika způsoby.
Nominální teplotní křivky
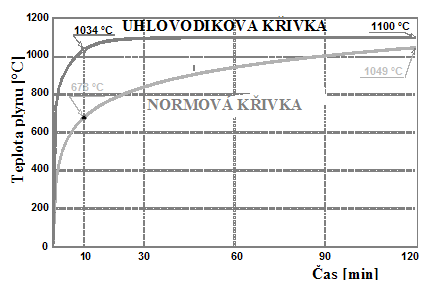
Obr. 1 Nominální normová a uhlovodíková teplotní křivka
Nominální normová teplotní křivka, definovaná v EN 1991-1-2, je základním z možných přístupů při výpočtu požární spolehlivosti konstrukcí. Dalšími nominálními křivkami uvedenými v normě jsou křivka vnějšího požáru a uhlovodíková křivka, viz obr. 1.
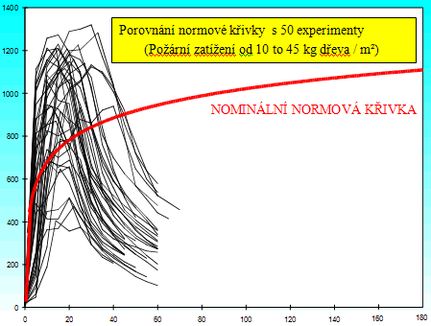
Obr. 2 Teplotní křivky přirozeného a normového požáru, viz [3]
Na obr. 2 jsou srovnány teplotní křivky přirozeného požáru pro různé konfigurace, tj. velikost požárního úseku, požární zatížení, izolace stěn, charakteristiky hořlavosti, a nominální normová požární křivka.
Z obrázku jsou zřejmé nepřesnosti při ověřování chování konstrukcí vystavených skutečnému požáru při uvažování nominální normové křivky. Některé faktory ovlivňující chování skutečného požáru nominální normová křivka neuvažuje.
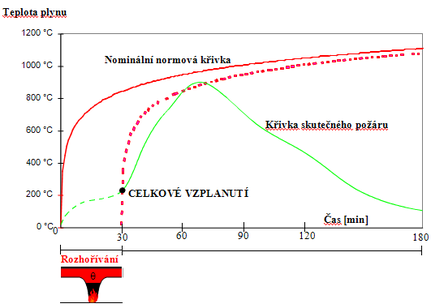
Obr. 3 Fáze požáru, viz [3]
Na obr. 3 jsou zachyceny fáze skutečného požáru, které zahrnují:
- fázi doutnání: zapálení a doutnající požár při velmi nízkých teplotách, jehož trvání lze obtížně odhadnout. Tato fáze není zachycena na obr. 3.
- fázi rozvoje: rozhořívání (lokální požár), jehož trvání závisí především na charakteristikách požárního úseku. Požár setrvává lokální až do případného celkového vzplanutí;
- okamžik celkového vzplanutí: lokální požár přechází v prostorový. Tato fáze je obecně velmi krátká.
- fázi plně rozvinutého požáru: trvání této fáze závisí na požárním zatížení a podmínkách ventilace.
- fázi dohořívání: pokles teplot nastává po vyhoření všech hořlavých materiálů.
Přirozené modely požáru
Z modelů požáru založených na fyzikálních parametrech se rozlišují tyto modely požáru:
- zjednodušené: převážně parametrické požáry, lokální požáry, je-li celkové vzplanutí požárního úseku nepravděpodobné
- zdokonalené: tyto modely uvažují všechny hlavní faktory ovlivňující požár jako je výměna plynu, hmotnostní výměna a energetická výměna. Jedná se o jednozónový model, dvouzónový model a výpočtové dynamické modely kapalin a plynů.
Jednozónový model uvažuje rovnoměrné rozdělení teplot v požárním úseku, zatímco dvouzónový proměnnou tloušťku horní vrstvy kouře s rovnoměrnou teplotou a dolní vrstvu o nižší teplotě.
Rozvoj požáru je ovlivněn rychlostí uvolňování tepla (RHR). Tato hodnota je určena velikostí požárního úseku, typem provozu v požárním úseku a časem. Ve fázi rozhořívání se jedná o požár lokální. Počátek této fáze je charakterizován rozvojem požáru, který lze popsat členem t2. Rychlost uvolňování tepla je tak popsána parabolicky. Provozy v budovách lze rozdělit do 4 kategorií podle rychlosti rozvoje požáru: pomalý, střední, rychlý a velmi rychlý. Rychlost uvolňování tepla dosáhne maximální hodnoty ve fázi ustáleného stavu hoření, které může být řízeno palivem nebo ventilací.
Rozhodující je informace o změně RHR v čase a stanovení, zda se požár rozvine v prostorový nebo zda zůstane lokální. Pokud nenastane okamžik celkového vzplanutí, požár setrvá lokální. V tomto případě lze použít dvouzónový výpočetní model. Účinky lokálního požáru lze určit dvouzónovým výpočetním modelem nebo empirickými modely vyvinutými při výzkumech pro modely požáru rozměrných požárních úseků, viz [5]. Tepelné účinky lokálního požáru řeší metoda HASEMI [6], která je založena na výsledcích pořízených při experimentech. Použitím obou zmíněných metod lze stanovit rozložení teplot v prostoru kolem lokálního požáru.
Charakteristiky požárního úseku
Pro výpočet je nezbytné znát charakteristiky budovy. Požární úsek se charakterizuje nejen geometrií, ale i tepelnými vlastnostmi dělících konstrukcí, které jsou schopny akumulace a velkého přenosu tepla získaného z požáru, a okenními otvory, které přivádějí vzduch z okolního prostoru. V postupech požárně bezpečnostního inženýrství je požární návrh obvykle založen na fyzikálním popisu tepelného zatížení. Ve srovnání s návrhovými postupy za běžných teplot, je při požárním návrhu rozhodující velikost požárního zatížení, rychlost uvolňování tepla a podmínky ventilace.
Hustota požárního zatížení
Hustota požárního zatížení vycházející z národní klasifikace provozů (statistický přístup) nebo ze speciálně provedeného rozboru požárního zatížení (deterministický přístup) je uvedena v příloze E normy ČSN EN 1991-1-2. Obvykle je požární zatížení stanoveno statisticky, pouze ve výjimečných případech je definováno deterministicky.
Deterministický přístup
Požární zatížení Q v požárním úseku je definováno jako celkové množství energie, které se může uvolnit v průběhu požáru. Část celkové energie je použita na zahřátí požárního úseku (dělících konstrukcí a vnitřního vzduchu), zbytek je odveden otvory. Jednotlivé součásti budovy jako jsou hořlavá obložení stěn, podlah a stropů nebo vybavení uvnitř budovy, jako je například nábytek, tvoří požární zatížení. Požární zatížení Q na jednotku plochy požárního úseku se nazývá hustota požárního zatížení qf.
V EN 1991-1-2 je charakteristická hodnota hustoty požárního zatížení uvažována podle vztahu:
kde
- Mk,i
- je množství hořlavého materiálu i [kg];
- Hui
- je čistá výhřevnost materiálu i [MJ/kg], viz tab. 1;
- Ψi
- je součinitel chráněného požárního zatížení pro materiál i;
- Af
- podlahová plocha požárního úseku [m2].
Hodnoty Hui a Mk,i představují celkové množství energie obsažené v materiálu i uvolněné pro hoření. Čistá výhřevnost dřeva Hu je 17,5 MJ/kg, případně 14 MJ/kg pro (m Hu).
Statistický přístup
Hustotu požárního zatížení lze určit deterministickým přístupem, tj. sečtením veškerého požárního zatížení v požárním úseku. Pro některé specifické provozy, jako jsou například kanceláře nebo školy, jsou hodnoty hustoty požárního zatížení známé. U provozů, kde se předpokládá podobné množství hustoty požárního zatížení, lze použít statistický přístup. V těchto případech je hustota požárního zatížení uvažována střední hodnotou.
Hodnoty hustoty požárního zatížení pro různé provozy jsou uvedeny v tab. 2. Pravděpodobnost dosažení hustoty požárního zatížení při požáru je zohledněna pomocí 80%, 90% a 95% kvantilu Gumbelova rozdělení s variačním koeficientem 0,3.
| Pevné látky | |
| Dřevo | 17,5 |
| Jiné celulózové materiály • Oděvy • Korek • Bavlna • Papír, lepenka • Hedvábí • Sláma • Vlna | 20 |
| Uhlíkaté látky • Antracit • Dřevěné uhlí • Uhlí | 30 |
| Chemické látky | |
| Parafínová řada • Methan • Ethan • Propan • Butan | 50 |
| Olefínová řada • Ethylen • Propylen • Butylen | 45 |
| Aromatická řada • Benzen • Toluen | 40 |
| Alkoholy • Methanol • Ethanol • Ethylalkohol | 30 |
| Paliva • Benzín, petrolej • Nafta | 45 |
| Čisté uhlovodíkové plasty • Polyethylen • Polystyren • Polypropylen | 40 |
| Ostatní výrobky | |
| ABS (plast) | 35 |
| Polyester (plast) | 30 |
| Polyizokyanát a polyuretan (plast) | 25 |
| Polyvinylchlorid, PVC (plast) | 20 |
| Živice, asfalt | 40 |
| Kůže | 20 |
| Linoleum | 20 |
| Gumové pneumatiky | 30 |
| POZNÁMKA: Hodnoty uvedené v této tabulce neplatí pro výpočet energetického obsahu paliv | |
| Odchylka | Průměr | 80% kvantil | 90% kvantil | 95% kvantil | |
|---|---|---|---|---|---|
| Byty | 234 | 780 | 948 | 1085 | 1217 |
| Nemocnice (pokoje) | 69 | 230 | 280 | 320 | 359 |
| Hotely (pokoje) | 93 | 310 | 377 | 431 | 484 |
| Knihovny | 450 | 1500 | 1824 | 2087 | 2340 |
| Kanceláře (standardní) | 126 | 420 | 511 | 584 | 655 |
| Školní třídy | 85,5 | 285 | 347 | 397 | 445 |
| Nákupní centra | 180 | 600 | 730 | 835 | 936 |
| Divadla (kina) | 90 | 300 | 365 | 417 | 468 |
| Doprava (veřejné prostory) | 30 | 100 | 122 | 139 | 156 |
Návrhovou hodnotu hustoty požárního zatížení lze stanovit jako
Součinitel m je bezrozměrné číslo, které se uvažuje v rozmezí od 0 do 1 a představuje účinnost hoření: m = 1 pro velmi hořlavé materiály a m = 0 pro materiály nehořlavé. Pro standardní celulózové materiály je m = 0,8.
Pravděpodobnost, že požár vznikne a postupně se rozšíří do plně rozvinutého stádia, závisí na charakteristikách požárního úseku a na přítomnosti aktivních, požárně bezpečnostních opatření jako jsou samočinná hasicí zařízení (spriklery), samočinné požární hlásiče (kouřové, tepelné), zařízení dálkového přenosu k požární jednotce a zásah požární jednotky. Tyto okolnosti zahrnují součinitele δq1, δq2 a δn. Součinitel δq1 a δq2 zohledňují nebezpečí vzniku požáru vlivem velikostí požárního úseku a typem provozu, a δn zohledňuje vliv aktivní požární ochrany, viz tab. 3.
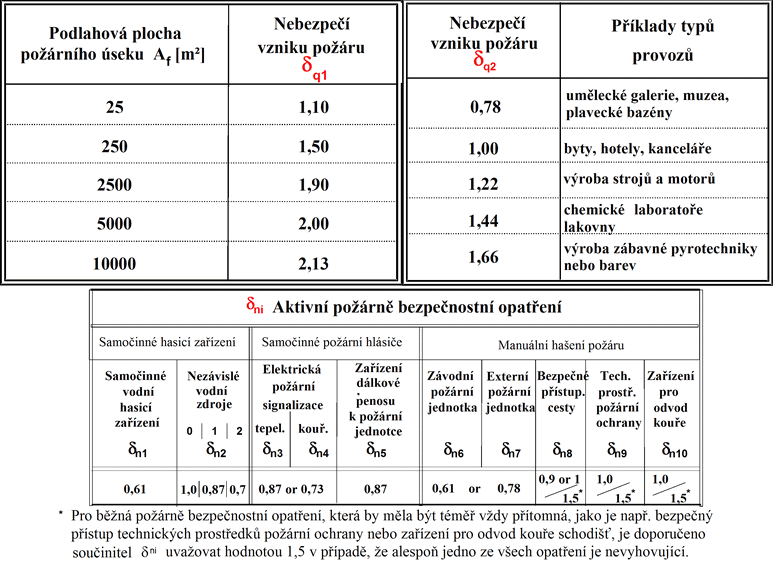
Tab. 3 Souhrnná tabulka součinitelů δ, viz [2]
Rychlost uvolňování tepla
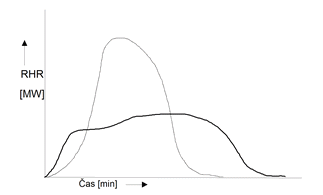
Obr. 4 Rozdílné průběhy rychlosti uvolňování tepla RHR pro stejné množství požárního zatížení a stejnou plochu požárního úseku
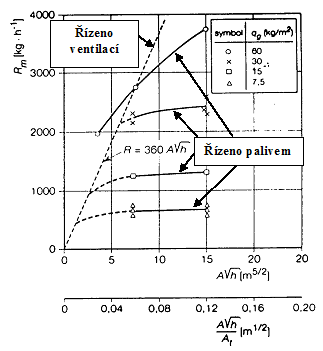
Obr. 5 Množství hořícího paliva v závislosti na podmínkách ventilace, viz [2]
Rozvoj a útlum požáru je ovlivněn rychlostí odhořívání požárního zatížení v čase. Tuto informaci poskytuje hodnota rychlosti uvolňování tepla RHR. Shodné požární zatížení může hořet velmi rychle nebo velmi pomalu, což vede k naprosto rozdílným teplotním křivkám, viz obr. 4.
Hodnota rychlosti uvolňování tepla RHR ovlivňuje průběh teplot plynů v čase. Fáze rozvoje, kdy z požáru malých rozměrů vzniká požár rozsáhlý, je závislá na množství kyslíku dostupného při hoření. Při dostatečném přístupu kyslíku do místa hoření je rychlost uvolňování tepla ovlivněna množstvím požárního zatížení v požárním úseku – požár řízen palivem. V případě malých ploch otvorů obvodových konstrukcí je rychlost uvolňování tepla ovlivněna nedostatečným množstvím kyslíku pro hoření – požár řízen ventilací. U obou případů dochází k rasantnímu nárůstu rychlosti uvolňování tepla RHR po celkovém vzplanutí. Tento okamžik určuje přechod mezi lokálním a prostorovým požárem, který pohltí veškeré hořlavé materiály požárního úseku. Porovnání požárů řízených palivem nebo ventilací, podle množství hořícího paliva v závislosti na podmínkách ventilace, je zobrazeno v následujícím grafu, viz obr 5. Hodnota Aw √h představuje podmínky ventilace, kde Aw je celková plocha otvorů a h výška otvorů. Každá křivka je sestrojena pro rozdílnou hustotu požárního zatížení. Z grafu je patrný přechod od požáru řízeného ventilací k požáru řízeného palivem. Se vzrůstající hodnotou Aw √h postupně vzrůstá množství hořícího paliva až do hodnoty maximálně dostupného požárního zatížení v požárním úseku.
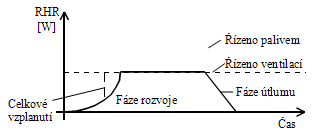
Obr. 6 Rychlost uvolňování tepla RHR v čase
Rychlost uvolňování tepla RHR ve fázi rozvoje, viz obr. 6, až do maximální hodnoty lze popsat:
(6)
kde
- Q
- je rychlost uvolňování tepla ve fázi rozvoje [W],
- t
- je čas [s],
- tα
- je doba potřebná pro dosažení rychlosti uvolňování tepla 1 MW [s].
Jak již bylo zmíněno, lze průběh požáru charakterizovat třemi fázemi: fází rozvoje, ustáleným stavem, fází útlumu. Rychlost rozvoje požáru závisí na typu provozu v požárním úseku, ale i na dalších okolnostech, viz obr. 7. Po fázi rozvoje následuje ustálený stav, kde hodnota RHR dosahuje svého maxima. Fáze útlumu hoření je vyjádřena lineárním poklesem RHR.
Na základě mnoha požárních experimentů bylo zjištěno, že počátek fáze útlumu nastává po vyhoření 70 % veškerého požárního zatížení v požárním úseku. Na následujícím obrázku je uveden návrh křivky RHR používané ve výzkumném projektu NFSC, viz obr. 7. Křivka zahrnuje fázi rozvoje, ustálený stav a fázi útlumu.
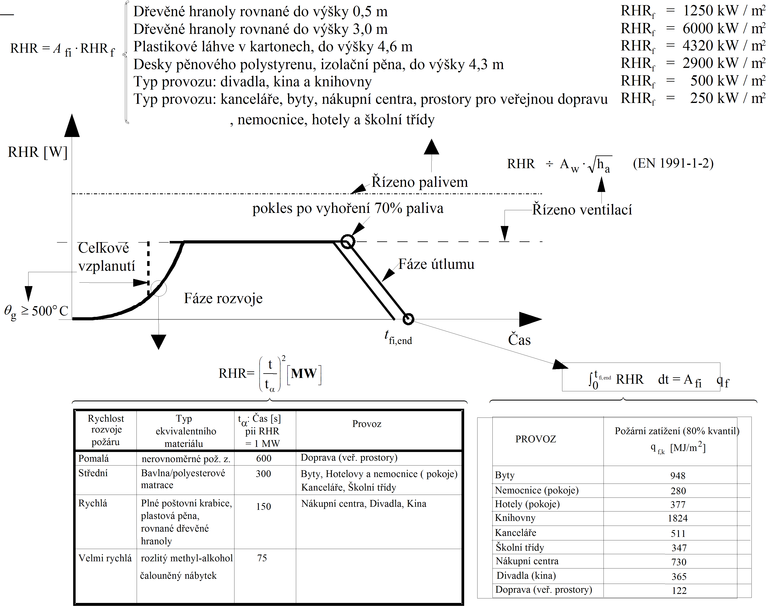
Obr. 7 Návrh RHR křivky, viz [2]
Experiment je dalším možným přístupem stanovení křivky RHR. Metoda experimentálního určení křivky RHR, známá již několik let, je založena na principu měření spotřeby kyslíku při požáru v požárním úseku.
V práci [3] je uveden postup, který definuje průběh požáru pomocí RHR křivek pro jednotlivé předměty nacházející se v požárním úseku. Databáze výsledků zahrnuje pouze omezený počet předmětů používaných především v obytných prostorech, jako jsou například židle, televizory nebo vánoční stromky. Toto omezení je vyváženo výhodou, která spočívá v důkladném popisu všech tří fází průběhu požáru. Hodnotným zdrojem informací je databáze “Initial Fires” [3], zpracovaná na University of Lund, která navazuje na databázi výsledků v [4]. Uvádí rozšířený počet předmětů užívaných v obytných prostorech i další předměty, jako jsou například různé typy automobilů. Na CTICM ve Francii byly uskutečněny požární experimenty pro zjištění RHR křivek nových automobilů (vyrobených v roce 1996), hotelových pokojů a nábytku.
Přirozené modely požáru
Zjednodušené výpočtové modely požáru pro fázi požáru před celkovým vzplanutím (modely lokálního požáru a dvouzónové modely) a fázi po celkovém vzplanutí (modely plně rozvinutého požáru – jednozónový model a parametrická teplotní křivka) jsou popsány v přílohách A, C a D normy ČSN EN 1991-1-2. Řešení pomocí prostorových modelů (např. CFD – Dynamická analýza plynů) jsou příliš složitá pro běžné použití, a proto jsou z této kapitoly vyjmuty.
Parametrická teplotní křivka
Parametrická teplotní křivka využívá pro popis rozvoje požáru v budově hlavních fyzikálních závislostí ovlivňujících hoření. Na rozdíl od nominální normové křivky je popis závislosti teploty v požárním úseku na čase doplněn o další parametry, které vystihují skutečný požár. Téměř všechny modely parametrických teplotních křivek popsaných v dostupné literatuře uvažují tyto parametry:
- geometrické charakteristiky požárního úseku;
- požární zatížení v požárním úseku;
- velikost otvorů v obvodových konstrukcích, střeše nebo stropu;
- typ obvodových konstrukcí, které tvoří hranice požárního úseku.
Parametrické křivky jsou založeny na předpokladu rovnoměrně rozložené teploty v celém prostoru požárního úseku, což omezuje jejich použití ve fázi po celkovém vzplanutí u požárních úseků běžných rozměrů. Přesto jsou tyto modely v porovnání s nominálními modely významným vylepšením při předpovědi rozložení teplot v požárním úseku. Výhodou je především snadný a rychlý analytický popis předpovědi, který nevyžaduje žádné sofistikované počítačové nástroje.
Návod pro výpočet parametrické teplotní křivky je obsažen v příloze A v EN 1991-1-2, který je omezen následujícími předpoklady: velikost podlahové plochy požárního úseku se uvažuje maximálně do 500 m2, ve střešní nebo stropní konstrukci se nenacházejí otvory, výška prostoru nepřesahuje 4 m, koeficient b je v rozmezí 1.000–2.200 J/m2s1/2K a součinitel O v rozmezí 0,02–0,20. Výpočet koeficientu b a součinitele O je popsán níže.
Rozvoj teploty plynů v požárním úseku je určen podle:
kde
At
(10)
kde
- t
- je čas [hod]
- Av
- celková plocha svislých otvorů [m2]
- h
- výška svislých otvorů [m]
- At
- celková plocha konstrukcí (stěn, stropu, podlahy, včetně otvorů) [m2]
- b
- koeficient povrchů [J/m2s1/2K], který je závislý na tepelné pohltivosti konstrukcí ohraničujících požární úsek (výpočet popsán dále)
Tepelné vlastnosti materiálů charakterizují tři hlavní parametry:
- měrné teplo cp
- hustota ρ
- tepelná vodivost λ
Tepelná vodivost a měrné teplo závisí na teplotě.
U zjednodušených výpočtů je tepelná pohltivosti konstrukce popsána koeficientem b, který je určen z tepelných vlastností materiálů rovnicí:
(11)
Při výpočtu koeficientu povrchu b lze hodnoty hustoty ρ, měrného tepla cp, a tepelné vodivosti λ uvažovat za běžných teplot, viz EN 1991-1-2.
V případě vícevrstvých konstrukcí je doporučeno hodnotu koeficientu b odvodit následovně:
- pro dvě rozdílné vrstvy s koeficienty b1 a b2, pro které platí b1 < b2, potom je výsledná hodnota součinitele b = b1;
- v případě, že platí b1 > b2, je počítána mezní tloušťka materiálu vystaveného požáru podle:
(12)
kde
- td
- je čas požáru až do fáze útlumu
Potom je koeficient b určen:
(14)
Tepelné vlastnosti při různých teplotách běžně používaných materiálů jsou uvedeny v tab. 4.
| Materiál | Teplota [°C] | λ [W/m/K] | ρ [kg/m3] | cp [J/kg°K] |
|---|---|---|---|---|
| Prostý beton | 20 | 2 | 2300 | 900 |
| 200 | 1,63 | 2300 | 1022 | |
| 500 | 1,21 | 2300 | 1164 | |
| 1000 | 0,83 | 2300 | 1289 | |
| Lehký beton | 20 | 1 | 1500 | 840 |
| 200 | 0,875 | 1500 | 840 | |
| 500 | 0,6875 | 1500 | 840 | |
| 1000 | 0,5 | 1500 | 840 | |
| Ocel | 20 | 54 | 7850 | 425 |
| 200 | 47 | 7850 | 530 | |
| 500 | 37 | 7850 | 667 | |
| 1000 | 27 | 7850 | 650 | |
| Rohože z křem. vláken | 20 | 0,035 | 128 | 800 |
| 200 | 0,06 | 128 | 900 | |
| 500 | 0,12 | 128 | 1050 | |
| 1000 | 0,27 | 128 | 1100 | |
| Těsnící tmel | 20 | 0,0483 | 200 | 751 |
| 250 | 0,0681 | 200 | 954 | |
| 500 | 0,1128 | 200 | 1052 | |
| 800 | 0,2016 | 200 | 1059 | |
| Křemíkové desky | 20 | 0,0685 | 450 | 748 |
| 250 | 0,0786 | 450 | 956 | |
| 450 | 0,0951 | 450 | 1060 | |
| 1050 | 0,157 | 450 | 1440 | |
| Dřevo | 20 | 0,1 | 450 | 1113 |
| 250 | 0,1 | 450 | 1125 | |
| 450 | 0,1 | 450 | 1135 | |
| 1050 | 0,1 | 450 | 1164 | |
| Zdivo | 20 | 1,04 | 2000 | 1113 |
| 200 | 1,04 | 2000 | 1125 | |
| 500 | 1,18 | 2000 | 1135 | |
| 1000 | 1,41 | 2000 | 1164 | |
| Sklo | 20 | 0,78 | 2700 | 840 |
Otvory v požárně dělící konstrukci můžou být tvořeny okny, dveřmi a stropními otvory. Průběh požáru je závislý na počtu a velikosti těchto otvorů. Součinitel otvorů O pro samostatný svislý otvor lze určit podle vzorce:
(15)
Pro více otvorů se uvažuje s celkovou plochou svislých otvorů a s váženým průměrem výšek otvorů podle:
(16)
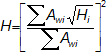(17)
kde
- Aw
- je plocha svislého otvoru,
- H
- je výška otvoru
- i
- je pořadové číslo otvoru.
Průběh fáze rozhořívání je určen podle:
kde
- qt,d
- je návrhová hodnota hustoty požárního zatížení pro At [MJ/m2]
- tlim
- 20 min, obdobný jako pro volné hoření τF podle přílohy B v ČSN EN 1991-1-2.
Podle tmax mohou nastat dva možné případy:
- buď je průběh fáze zahřívání vypočtené podle prvního členu rovnice, 0,2 × 10−3 qt,d / O, delší než limitní hodnota času tlim. Potom je výpočet uvažován bez jakýchkoliv úprav.
- nebo je průběh fáze zahřívání vypočtené podle prvního členu rovnice, 0,2 × 10−3 qt,d / O, kratší než limitní hodnota času tlim. V tomto případě je výpočet modifikován koeficientem otvorů Olim, který lze vyjádřit jako:
tmax je modifikován následujícím způsobem:
(19)
(20)
kde
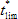
- nahrazuje v rovnici parametrické křivky hoření hodnotu t*.
Vliv ventilace během fáze zahřívání, v případě že td = tlim, lze popsat:
(22)
(23)
Teplotní křivka ve fázi chladnutí je dána vztahy:
≤ 0,5
≤ 2,0
kde
- Θmax
- je největší teplota na konci fáze zahřívání podle parametrické rovnice hoření,
kde t = td.
Příklad stanovení parametrické požární křivky je zobrazen na následujícím obrázku, požární zatížení qt,d = 180 MJ/m2, b = 1.160 J/m2s1/2K, koeficient otvorů O se uvažuje v rozsahu od 0,04 m1/2 do 0,20 m1/2.
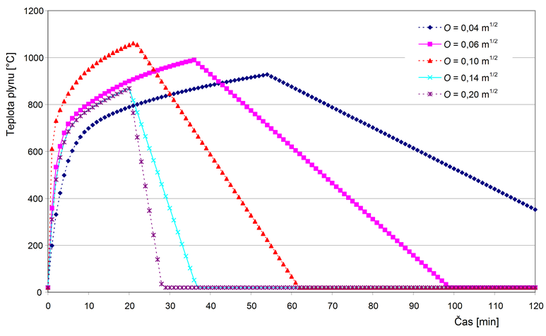
Obr. 8 Příklady parametrických požárních křivek
Lokální požáry
Při lokálním požáru je prostor požárního úseku horizontálně rozdělen do horní horké vrstvy, kde dochází k hromadění zplodin hoření, a do spodní vrstvy, kde je teplota plynů mnohem nižší.
Tento případ požáru lze velmi dobře popsat dvouzónovými modely. Kromě předpovědi vývoje teploty plynů tyto modely poskytují informace o šíření kouře v budově a bezpečnosti osob v budově v závislosti na tloušťce horní vrstvy kouře, množství toxických plynů, hustotě tepelného toku a optické hustoty.
Horizontální části konstrukce situované nad požárem jsou ovlivněny tepelným zatížením, které závisí především na vzdálenosti povrchů konstrukce od plamenů. Výpočtem účinků lokálního požáru na okolní konstrukce se zabývají metody Heskestad a Hasemi, viz [6].
Metoda Heskestad
Tepelné zatížení lokálního požáru řeší metoda Heskestad EN 1991-1-2. Rozlišují se dva případy podle relativní délky plamene vůči stropu.
Délka plamene Lf lokálního požáru, viz obr. 9, je dána vztahem:
Pokud plameny nezasahují strop požárního úseku, Lf < H; viz obr. 9, nebo v případě požáru ve volném prostoru, je teplota Θ(z) v oblaku hořících plynů po výšce svislé osy dána vztahem:
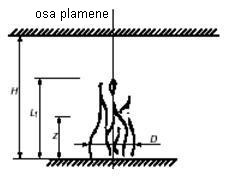
Obr. 9 Model lokálního požáru pro případ, kdy plameny nezasahují strop
kde
- D
- je průměr ohně, viz obr. 9, [m]
- Q
- je rychlost uvolňování tepla při požáru [W]
- Qc
- je část rychlosti uvolňování tepla při požáru sdílená prouděním [W], lze uvažovat Qc = 0,8 Q
- z
- je proměnná výška plamene podél osy plamene [m]
- H
- je svislá vzdálenost mezi stropem a zdrojem požáru, viz obr. 9, [m]
Metoda Hasemi
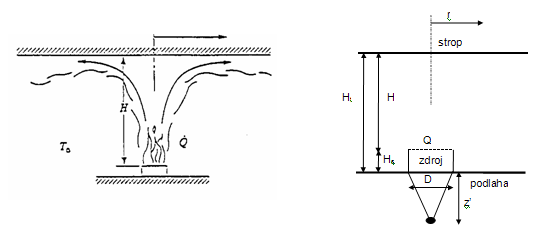
Obr. 10 Model lokálního požáru pro případ, kdy plameny zasahují strop
Metoda Hasemi je jednoduchý nástroj pro zhodnocení účinků lokálního požáru na vodorovné prvky konstrukcí nad požárem. Je založena na výsledcích experimentů uskutečněných na „Building Research Institute“ v Tsukubě v Japonsku.
Potřebné údaje pro použití metody jsou:
- Q
- je rychlost uvolňování tepla při požáru [W]
- Hf
- svislá vzdálenost mezi stropem a podlahou [m]
- D
- průměr ohně [m]
- Hs
- svislá vzdálenost mezi podlahou a ohniskem zdroje požáru [m]
Proměnné:
- H
- je svislá vzdálenost mezi stropem a zdrojem požáru [m]
- Q*
- součinitel rychlosti uvolňování tepla při požáru [-]
- Q*H
- součinitel rychlosti uvolňování tepla při požáru [-]
- z´
- svislá poloha virtuálního zdroje tepla [m]
- LH
- vodorovná délka plamene v místě stropu [m]
- r
- vodorovná vzdálenost mezi osou ohně a bodem u stropu [m]
Postup výpočtu:
Stanovení LH pomocí hodnoty stanovené předchozím vztahem a z hodnoty H
Stanovení tepelného toku q’’ v [kW/m2] ve vzdálenosti r, podle
Pokles tepelného toku q’’, který dopadá na povrch stropu, je funkcí součinitele y a jeho růst závisí na Q. Obě funkce jsou zobrazeny na obr. 11 pro r = 0, H = 5 m, D = 3 m.
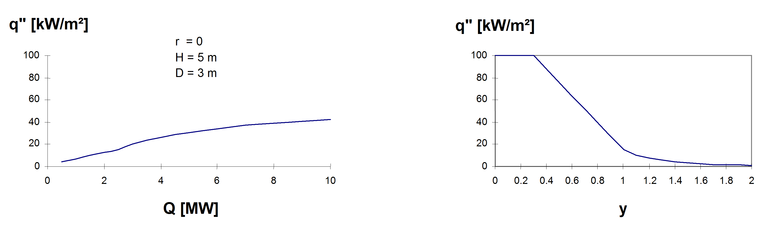
Obr. 11 Závislost tepelného toku q’’ na y a Q
Zónové modely
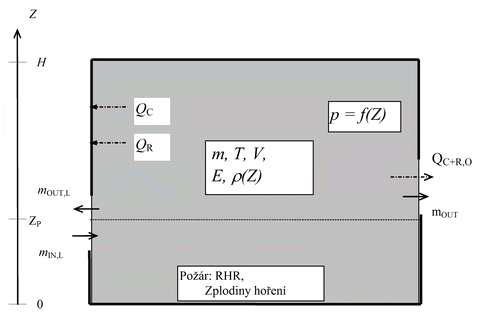
Obr. 12 Požární úsek vyšetřovaný jednozónovým modelem požáru
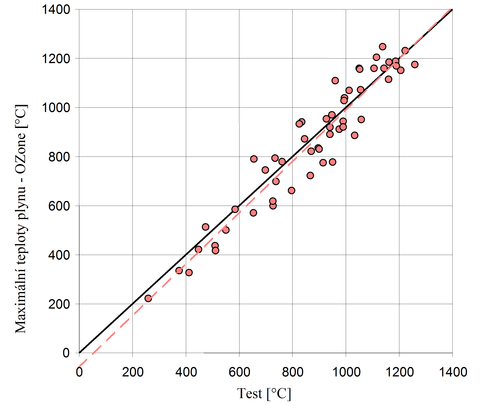
Obr. 13 Porovnání teplot plynu naměřených a vypočtených programem OZone
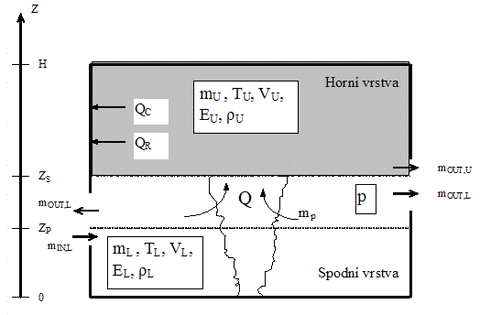
Obr. 14 Rozdělení požárního úseku do vrstev
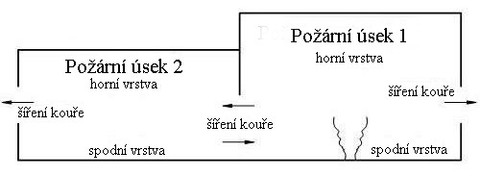
Obr. 15 Šíření hmoty a energie mezi požárními úseky
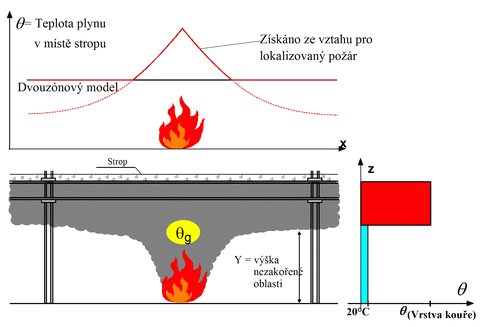
Obr. 16 Kombinace dvouzónového modelu s modelem lokálního požáru, viz [3]
Zónový model je název pro numerické řešení rozvoje teploty plynů v čase integrací obyčejných diferenciálních rovnic, které vyjadřují zachování hmoty a energie v každé vrstvě (zóně) požárního úseku. Je založen na předpokladu rovnoměrné teploty plynů v každé vrstvě. Pomocí zónových modelů lze, kromě rozvoje teploty plynů v čase, rovněž určit rozvoj teploty okolních konstrukcí nebo únik plynů otvory obvodových konstrukcí.
Údaje potřebné pro výpočet zónovým modelem:
- geometrické charakteristiky – rozměry požárního úseku, otvorů a dělících příček;
- materiálové charakteristiky obvodových konstrukcí požárního úseku,
- charakteristiky požáru – RHR křivka, rychlost tepelného rozkladu, teplo při hoření paliva.
Rozsah použití dvouzónového modelu je zaměřen především na fázi před celkovým vzplanutím. Pro předpověď rozvoje teplot u plně rozvinutého požáru je vhodnější použít jednozónový model.
Jednozónový model
Jednozónové modely požáru jsou platné pro fázi po celkovém vzplanutí a jsou založeny na předpokladu rovnoměrné teploty plynu v celém požárním úseku v průběhu požáru. Vstupní údaje potřebné pro výpočet jsou shodné s údaji u dvouzónových modelů. V porovnání se vstupy pro parametrické předpovědní křivky jsou podrobnější. Na následujícím obrázku je zobrazen jednozónový model požárního úseku.
V rámci projektů ECSC a NFSC 1 & 2 byl na University of Liège společně s Profilarbed Research vyvinut program OZone, který je založen na principu zónových modelů. Tento software byl využit pro porovnání s výsledky 54 experimentů. Na obr. 13 jsou porovnány největší teploty plynu v požárním úseku změřené při experimentech s vypočtenými v programu OZone. Body v grafu představují výsledky experimentů a plná úsečka jejich ideální polohu podle programu OZone. Pomocí lineární regrese byla proložena všemi body přímka, viz čárkovaná úsečka.
Dvouzónový model
Každá vrstva požárního úseku je popsána pomocí rovnic vyjadřujících rovnováhu zachování energie. Řešení přináší informace o rozvoji teplot plynů v každé ze dvou vrstev, rozvoji teploty okolních konstrukcí a úniku plynů otvory v obvodových konstrukcích. Důležitou informací je změna tloušťky vrstev v čase. Znalost tloušťky spodní vrstvy, která je chladnější a neobsahuje škodlivé látky vzniklé při hoření, je nezbytná pro stanovení možnosti úniku osob z požárního úseku v případě požáru. Rozdělení požárního úseku do vrstev s rozdílnými charakteristikami je uvedeno na obr. 14.
Na obr. 14 je zachycen typický případ požárního úseku, kdy dochází k výměně hmoty a energie pouze s okolním prostředím. Tyto modely však umožňují řešit i mnohem složitější případy, při kterých dochází nejenom k výměně hmoty a energie s okolním prostředím, ale i s okolními požárními úseky obklopující zkoumaný požární úsek. Lze tak snadno určit šíření kouře do ostatních požárních úseků. Takový případ je zachycen na obr. 15.
Kombinace dvouzónového modelu a modelu lokálního požáru
Rozložení teplot plynů v požárním úseku při lokálním požáru lze předpovědět dvouzónovým modelem. Tento model předpokládá rovnoměrnou teplotu v každé uvažované vrstvě. Předpoklad rovnoměrné teploty v teplejší vrstvě je dostatečně výstižný pro stanovení množství kouře vzniklého v požárním úseku, pravděpodobnosti celkového vzplanutí, kolapsu střešní nebo stropní konstrukce, atd. Při výpočtu chování části konstrukce přímo nad zdrojem požáru není předpoklad rovnoměrné teploty dostatečně výstižný, a proto se doporučuje dvouzónový model kombinovat s modelem lokálního požáru. Ve výpočtu jsou teploty v těsné blízkosti posuzované konstrukce, pro každý bod podél konstrukčního prvku, uvažovány největší hodnotou z obou předpovědních modelů.
Kombinace jednozónových a dvouzónových modelů, výběr modelu
Pokud byly stanoveny všechny potřebné charakteristiky požáru, jako jsou např. křivka RHR, geometrické údaje požárního úseku nebo charakteristiky dělících konstrukcí, je dalším nezbytným krokem správný výběr modelu podle uvažovaného požárního scénáře. Výběr závisí na rozsahu oblasti použití každého z modelů. Obvykle jsou počáteční fáze požáru modelovány pomocí dvouzónového modelu, který v určitém okamžiku přechází v jednozónový model. Otázkou je, kdy a jak tento přechod nastává.
Dvouzónový model požáru poskytuje dvě základní hodnoty:
- teplotu horní vrstvy v požárním úseku Tu;
- tloušťky obou vrstev Hi.
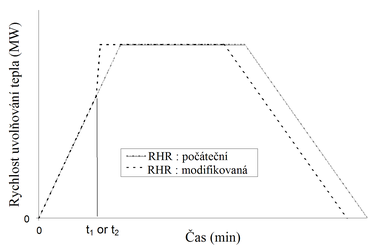
Obr. 17 Návrh křivky rychlosti uvolňování tepla RHR při požáru
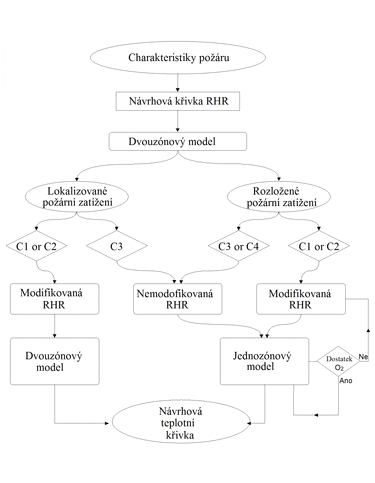
Tyto hodnoty určují rozsah aplikace modelu. Použití dvouzónového modelu je omezeno následujícími podmínkami, viz obr. 18:
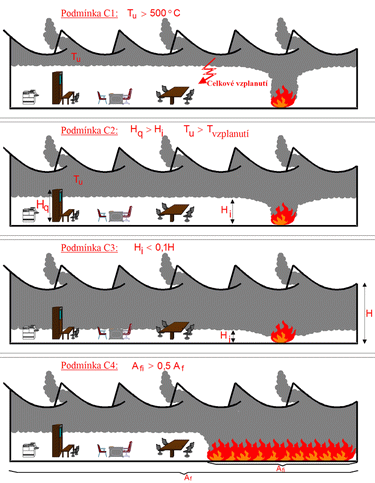
- Podmínka 1 (C1): Tu > 500 °C; vysoká teplota zplodin hoření (vyšší než 500 °C) vede k celkovému vzplanutí veškerého požárního zatížení vlivem sálání.
- Podmínka 2 (C2): Hi < Hq a Tu > Tignition ; pokud dojde ke snížení tloušťky spodní vrstvy (Hi) tak, že hořlavé materiály se nacházejí v horní vrstvě kouře, a pokud je v horní vrstvě vysoká teplota (vyšší než Tignition , kolem 300 °C), potom dojde k šíření požáru samovznícením.
- Podmínka 3 (C3): Hi < 0,1 H; tloušťka spodní vrstvy je minimální, což neodpovídá předpokladu dvouzónového modelu.
- Podmínka 4 (C4): Afi > 0,5 Af ; velikost hořící plochy je v porovnání s celkovou plochou požárního úseku tak velká, že se již nejedná o lokální požár.
V případě splnění podmínek 1 a 2 se přistupuje k modifikaci rychlosti uvolňování tepla RHR v počáteční fázi (popis dvouzónovým modelem) pro popis jednozónovým modelem. Příklad modifikace je uveden na obr. 17.
Výše zmíněný postup výpočtu je shrnut ve vývojovém diagramu na obr. 18.
Obr. 18 Kombinace jednozónového a dvouzónového modelu, viz [2]Mechanické zatížení
Stanovení mechanického zatížení vychází z návrhu při běžné teplotě, pokud je pravděpodobné, že bude působit i v požární situaci. Pro mimořádné návrhové situace se kombinace mechanického zatížení uvažuje podle vztahů podle ČSN EN 1990:
(39)
kde
- Gk,j
- je charakteristická hodnota stálého zatížení
- Qk,1
- charakteristická hodnota hlavního proměnného zatížení
- Qk,i
- charakteristická hodnota vedlejšího proměnného zatížení
- ψ1,1
- součinitel pro častou hodnotu proměnného zatížení
- ψ2,i
- součinitel pro kvazistálou hodnotu proměnného zatížení
Doporučené hodnoty součinitelů ψ1 a ψ2 jsou uvedeny v tabulce A1.1 v ČSN EN 1990, viz tab. 5. V národní příloze ČSN EN 1991-1-2 jsou tyto hodnoty upraveny.
| Zatížení | ψ0 | ψ1 | ψ0 |
|---|---|---|---|
| Kategorie užitných zatížení pro pozemní stavby, viz norma (ČSN EN 1991-1-1: 2004) Kategorie A: obytné plochy Kategorie B: kancelářské plochy Kategorie C: shromažďovací plochy Kategorie D: obchodní plochy Kategorie E: skladovací plochy |
0,7 0,7 0,7 0,7 1,0 |
0,5 0,5 0,7 0,7 0,9 |
0,3 0,3 0,6 0,6 0,8 |
| Kategorie F: dopravní plochy, tíha vozidla ≤ 30 kN Kategorie G: dopravní plochy, 30 kN < tíha vozidla ≤ 160 kN Kategorie H: střechy | 0,7 0,7 0 | 0,7 0,5 0 | 0,6 0,3 0 |
| Zatížení sněhem, viz norma (ČSN EN 1991-1-3: 2004) Finsko, Island, Norsko, Švédsko Ostatní členové CEN, pro stavby umístěné ve výšce H > 1000 m n.m. Ostatní členové CEN, pro stavby umístěné ve výšce H ≤ 1000 m n.m. |
0,7 0,7 0,5 |
0,5 0,5 0,2 |
0,2 0,2 0 |
| Zatížení větrem, viz norma (ČSN EN 1991-1-4: 2004) | 0,6 | 0,2 | 0 |
| Teplota (ne od požáru) pro pozemní stavby, viz norma (ČSN EN 1991-1-5: 2004) | 0,6 | 0,5 | 0 |
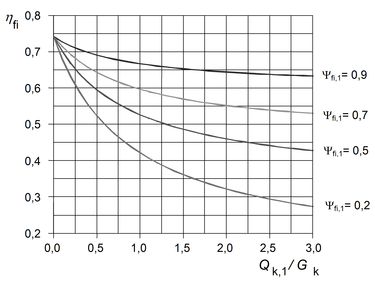
Obr. 19 Závislost redukčního součinitele ηfi,t na poměru Qk,1 / Gk a součiniteli ψ1,1
Nepřímá zatížení konstrukce v důsledku roztažení a přetvoření, způsobená teplotními změnami od požáru, vyvolávají síly a momenty. Nepřímá zatížení lze uvažovat obvykle pouze pokročilou globální analýzou za zvýšené teploty. Nepřímá zatížení od požáru není nutno při výpočtu konstrukce uvažovat, pokud jsou zanedbatelná, příznivá nebo je konzervativně zvolený model podepření a okrajových podmínek. Při hodnocení nepřímých zatížení se má uvažovat vynucené tepelné roztažení vlastních prvků, rozdílné tepelné roztažnosti staticky neurčitých prvků, teplotní gradienty v průřezech, tepelné roztažení sousedních prvků.
Důležitou veličinou používanou při požárním návrhu podle EN 1991-1-2 je redukční součinitel účinku zatížení při požární situaci ηfi,t, který je definován jako 
, kde Ed je návrhový účinek zatížení při pokojové teplotě a Ed,fi je návrhový účinek zatížení při zvýšené teplotě. Redukční součinitel lze určit rovněž podle následujícího vztahu:
(40)
kde
- γQ,1
- je dílčí součinitel pro hlavní proměnné zatížení.
Redukční součinitel ηfi,t závisí především na součiniteli ψ1,1, který se mění podle kategorie zatížení v budově. V ČSN EN 1993-1-2 (část pro požární zatížení ocelových konstrukcí) a ČSN EN 1994-1-2 (část pro požární zatížení spřažených konstrukcí) je uveden graf závislosti ηfi,t na poměru Qk,1 / Gk a součiniteli ψ1,1, viz obr. 19.
Národní příloha k ČSN EN 1991-1-2
Národní příloha normy ČSN EN 1991-1-2 je informativní, národně stanovené parametry, kterých je deset, mají pro stavby umístěné na území České republiky normativní charakter. Prvních devět národně stanovených parametrů uplatňuje hodnoty doporučené v jednotlivých článcích normy. Článek NA 2.10 uvádí, že se v ČR pro reprezentativní hodnotu proměnného zatížení Q1 má použít její kvazistálá hodnota ψ2,1 ‧ Q1. Podle charakteru konstrukce budovy a jejího umístění se doporučuje, zejména u halových objektů, pro zatížení větrem a větrem během požáru použít častou hodnotu zatížení ψ1,1 ‧ Q1. Doporučené hodnoty součinitelů ψ1,1 a ψ2,1 jsou uvedeny v normě ČSN EN 1990, tabulka A1.1.
Symboly v ČSN EN 1991-1-2
- A
- plocha požárního úseku
- Aind,d
- návrhová hodnota nepřímého zatížení vyvolaného požárem
- Af, Afi
- podlahová plocha požárního úseku, plocha požáru
- Ah
- plocha vodorovných otvorů ve střeše požárního úseku
- Ah,v
- celková plocha otvorů v konstrukcích ohraničujících požární úsek (Ahv = Ah + Av)
- Aj
- plocha povrchu j-té konstrukce ohraničující požární úsek, bez otvorů
- At
- celková plocha konstrukcí ohraničujících požární úsek (stěny, strop a podlaha, včetně otvorů)
- Av
- celková plocha svislých otvorů ve všech stěnách (Av =
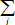Av,i) - Av,i
- plocha i-tého okna
- Ci
- součinitel ochrany i-té povrchové plochy prvku
- D
- hloubka požárního úseku; průměr požáru
- Ed
- návrhová hodnota příslušných účinků zatížení ze základní kombinace podle EN 1990
- Efi,d
- konstantní návrhová hodnota příslušných účinků zatížení při požární situaci
- Efi,d,t
- návrhová hodnota příslušných účinků zatížení při požární situaci v čase t
- Eg
- vnitřní energie plynu
- H
- vzdálenost mezi zdrojem požáru a stropem
- Hu
- hodnota čisté výhřevnosti včetně vlhkosti
- Hu0
- hodnota čisté výhřevnosti suchého materiálu
- Hui
- hodnota čisté výhřevnosti i-tého materiálu
- Lc
- délka jádra
- Lf
- délka plamene podél osy
- LH
- vodorovný průmět plamene (z fasády)
- Lh
- vodorovná délka plamene
- LL
- výška plamene (od horní části okna)
- Lx
- délka osy od okna k bodu, pro který se provádí výpočet
- Mk,i
- množství i-tého hořlavého materiálu
- O
- faktor otvorů požárního úseku (O = Av
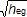/ At ) - Olim
- redukovaný faktor otvorů v případě požáru řízeného palivem
- Pint
- vnitřní tlak
- Q
- rychlost uvolňování tepla při požáru
- Qc
- konvekční část rychlosti uvolňování tepla Q
- Qfi,k
- charakteristické požární zatížení
- Qfi,k,i
- charakteristické požární zatížení i-tým materiálem
- Q*D
- součinitel uvolňování tepla vztažený na průměr D lokálního požáru
- Q*H
- součinitel uvolňování tepla vztažený na výšku H požárního úseku
- Qk,1
- charakteristická hodnota hlavního proměnného zatížení
- Qmax
- maximální rychlost uvolňování tepla
- Qin
- rychlost uvolňování tepla vstupujícího otvory vlivem proudění plynů
- Qout
- úbytek rychlosti uvolňování tepla vlivem proudění plynů vystupujících z otvorů
- Qrad
- úbytek rychlosti uvolňování tepla vlivem sálání z otvorů
- Qwall
- úbytek rychlosti uvolňování tepla sáláním a prouděním na povrchové plochy požárního úseku
- R
- konstanta ideálního plynu (= 287 J/kgK)
- Rd
- návrhová hodnota únosnosti prvku při normální teplotě
- Rfi,d,t
- návrhová hodnota únosnosti prvku při požární situaci v čase t
- RHRf
- maximální rychlost uvolňování tepla na metr čtvereční
- T
- teplota [K]
- Tamb
- teplota okolí [K]
- T0
- počáteční teplota (= 293 K)
- Tf
- teplota v požárním úseku [K]
- Tg
- teplota plynu [K]
- Tw
- teplota plamene u okna [K]
- Tz
- teplota plamene podél jeho osy [K]
- W
- šířka stěny s okny (W1 a W2)
- W1
- šířka stěny 1, u které se předpokládá největší plocha oken
- W2
- šířka stěny požárního úseku, kolmé ke stěně W1
- Wa
- vodorovný průmět markýzy nebo balkonu
- Wc
- šířka jádra
- b
- tepelná pohltivost celé ohraničující konstrukce (b =
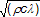) - bi
- tepelná pohltivost i-té vrstvy povrchové plochy jedné ohraničující konstrukce
- bj
- tepelná pohltivost povrchové plochy j-té ohraničující konstrukce
- c
- specifické teplo
- deq
- geometrická charakteristika vnějšího nosného prvku (průměr nebo strana)
- df
- tloušťka plamene
- di
- rozměr i-té povrchové plochy prvku
- g
- gravitační zrychlení
- heq
- vážený průměr výšky oken ve všech stěnách (heq = ( 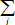(Av,i hi) ) / Av)
- hi
- výška i-tého okna
- ḣ
- tepelný tok na jednotku plochy povrchu
- ḣ net
- čistý tepelný tok na jednotku plochy povrchu
- ḣ net,c
- čistý tepelný tok na jednotku plochy povrchu vlivem proudění
- ḣ net,r
- čistý tepelný tok na jednotku plochy povrchu vlivem sálání
- ḣ tot
- celkový tepelný tok na jednotku plochy povrchu
- ḣ i
- tepelný tok na jednotku plochy povrchu vlivem i-tého požáru
- k
- opravný součinitel
- kb
- převodní součinitel
- kc
- opravný součinitel
- m
- hmotnost; součinitel hoření
- ṁ
- rychlost toku hmoty (pohybu plynů)
- ṁ in
- rychlost hmoty plynu vstupujícího otvory
- ṁ out
- rychlost hmoty plynu odcházejícího otvory
- ṁ fi
- rychlost vytváření produktů pyrolýzy
- q f
- požární zatížení vztažené na jednotku podlahové plochy Af
- qf,d
- návrhová hustota požárního zatížení vztažená na podlahovou plochu Af
- qf,k
- charakteristická hustota požárního zatížení vztažená na podlahovou plochu Af
- qt
- požární zatížení vztažené na jednotku plochy povrchů At
- qt,d
- návrhová hustota požárního zatížení vztažená na plochu povrchů At
- qt,k
- charakteristická hustota požárního zatížení vztažená na plochu povrchů At
- r
- vodorovná vzdálenost mezi svislou osou požáru a bodem u stropu, pro který se počítá tepelný tok
- si
- tloušťka i-té vrstvy
- slim
- mezní tloušťka
- t
- čas
- te,d
- ekvivalentní doba vystavení účinkům požáru
- tfi,d
- návrhová doba požární odolnosti (vlastnost prvku nebo konstrukce)
- tfi,requ
- požadovaná doba požární odolnosti
- tlim
- doba pro dosažení maximální teploty plynů v případě požáru řízeného palivem
- tmax
- doba pro dosažení maximální teploty plynů
- tα
- součinitel rychlosti rozvoje požáru
- u
- rychlost větru; vlhkost
- wi
- šířka i-tého okna
- wt
- součet šířek oken ve všech stěnách (wt = Σ wi); součinitel odvětrání vztažený k At
- wf
- šířka plamene; součinitel odvětrání
- y
- součinitel; parametr
- z
- výška
- z0
- virtuální počátek výšky z
- z´
- svislá poloha virtuálního zdroje tepla
- Φ
- polohový faktor
- Φf
- celkový polohový faktor prvku pro přenos tepla z otvoru sáláním
- Φf,i
- polohový faktor i-té povrchové plochy prvku pro daný otvor
- Φz
- celkový polohový faktor prvku pro přenos tepla z plamene sáláním
- Φz,i
- polohový faktor i-té povrchové plochy prvku pro daný plamen
- Γ
- časově závislá funkce faktoru otvorů O a tepelné pohltivosti b
- Γlim
- časově závislá funkce faktoru otvorů Olim a tepelné pohltivosti b
- Θ
- teplota [°C]; Θ [°C] = T [K] − 273
- Θcr,d
- návrhová hodnota kritické teploty materiálu [°C]
- Θd
- návrhová hodnota teploty materiálu [°C]
- Θg
- teplota plynu v požárním úseku, nebo v blízkosti prvku [°C]
- Θm
- teplota povrchu prvku [°C]
- Θmax
- maximální teplota [°C]
- Θr
- účinná teplota sálání prostředí požáru [°C]
- Ω
- (Af qf,d) / (Av At)1/2
- Ψi
- součinitel pro chráněné požární zatížení
- αc
- součinitel přestupu tepla prouděním
- αh
- plocha vodorovných otvorů vztažená na podlahovou plochu
- αv
- plocha svislých otvorů vztažená na podlahovou plochu
- δni
- součinitel, kterým se uvažuje existence i-tého specifického hasicího zařízení
- δq1
- součinitel, kterým se uvažuje nebezpečí vzniku požáru vzhledem k velikosti úseku
- δn2
- součinitel, kterým se uvažuje nebezpečí vzniku požáru vzhledem k druhu provozu
- εm
- povrchová emisivita prvku
- εf
- emisivita plamenů, ohně
- ηfi
- redukční součinitel
- ηfi,t
- úroveň zatížení pro návrhový požár
- λ
- tepelná vodivost
- ρ
- hustota
- ρg
- hustota vnitřního plynu
- σ
- Stephan-Boltzmannova konstanta (= 5,67 . 10−8 [W/m2K4])
- τF
- doba volného hoření ohně (předpokládá se 1 200 [s])
- ψ0
- součinitel kombinace pro charakteristickou hodnotu proměnného zatížení
- ψ1
- součinitel kombinace pro častou hodnotu proměnného zatížení
- ψ2
- součinitel kombinace pro kvazistálou hodnotu proměnného zatížení
Literatura
- [1] Wald F. a kol.: Výpočet požární odolnosti stavebních konstrukcí, České vysoké učení technické v Praze, Praha 2005, 336 s., ISBN 80-0103157-8.
- [2] Vassart O., Cajot L.G., Brasseur M., Strejček M.: Tepelná a mechanická zatížení, Difisek+, RFS-P2-06065, 2008, ČVUT v Praze.
- [3] Initial Fires: Lund University, Sweden. Institute of Fire Safety Engineering. ISSN 1102-8246. ISRN LUTVDG/TVBB--3070—SE, 1993.
- [4] Peacock, Jones, Bukowski and Forney. NIST Handbook 146, Volume II – Technical Reference Guide for the Hazard I Fire Hazard Assessment Method, 1991.
- [5] “Development of design rules for steel structures subjected to natural fires in Large Compartments”; Final report CEC Agreement 7210/ SA210, 317,517,618,832-February 1997.
- [6] Hasemi Y. and Tokunaga Tazo: “Flame Geometry Effects on the Buoyant Plumes from Turbulent Diffusion Flames”. Fire Science and Technology, Vol.4, N°1, 1984.
- [7] Ptchelintsev A., Hasemi Y., Nikolaenko M.,“Numerical Analysis of Structures exposed to localized Fire”, ASIAFLAM’s 95, Hong Kong, 1995.
- [8] Wakamatsu T., Hasemi Y., Yokobayashi Y., Ptchelintsev A.: “Experimental Study on the Heating Mechanism of a Steel Beam under Ceiling exposed to a localized Fire”.
- [9] Hasemi Y., Yokobayashi Y. , Wakamatsu T., Ptchelintsev A.: “Fire Safety of Building Components Exposed to a Localized Fire" – Scope and Experiments on Ceiling/Beam System Exposed to a Localized Fire, ASIAFLAM’s 95, Hong Kong, 1995.
Determination of the development of fire in the compartment with subsequent detection of temperature in different parts of the structure requires knowledge of many parameters. The most important step is to determine the design fire scenario that matches the extraordinary fire situation best. The design of fire can describe the temperatures in the fire department and determine the heat transfer in structure. Let's look at several models and the thermal and mechanical load of structures.
